Question

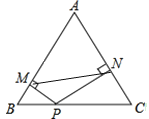
【题目】如图所示，点P是等边△ABC的BC边上一点，PM⊥AB，PN⊥AC，试猜想△AMN的周长L△AMN与四边形BMNC的周长L四边形BMNC有什么关系，并说明理由.

Answer 1

【答案】△AMN的周长与四边形BMNC的周长相等，理由见解析．

【解析】

依据∠BPM＝∠CPN＝30°，即可得出BM＝BP，CN＝CP，进而求得L△AMN＝AM＋AN＋MN＝BC＋MN；L四边形BMNC＝BM＋CN＋BC＋MN＝BC＋MN；+

即可得到△AMN的周长与四边形BMNC的周长相等．

解：△AMN的周长与四边形BMNC的周长相等．

∵△ABC为等边三角形，

∴AB＝AC＝BC，∠A＝∠B＝∠C＝60°，

又∵PM⊥AB，PN⊥AC，

∴∠BMP＝∠CNP＝90°，

∴∠BPM＝∠CPN＝30°，

∴BM＝BP，CN＝CP，

∴L△AMN＝AM+AN+MN

＝（AB﹣BM）+（AC﹣CN）+MN

＝（AB+AC）﹣（BM+CN）+MN

＝2BC﹣（PB+PC）+MN

＝2BC﹣BC+MN

＝BC+MN；

L四边形BMNC＝BM+CN+BC+MN

＝（PB+PC）+BC+MN

＝BC+BC+MN

＝BC+MN；

∴L△AMN＝L四边形BMNC．