题目内容
【题目】已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.

【答案】∠COD=5°或∠COD=125°.
【解析】
分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况进行解答,当射线OC在∠AOB的内部时,设∠AOC=2x,则∠COB=3x,计算出x的值,进而计算出∠AOC、∠AOD的度数,从而得出结论.当射线OC在∠AOB的外部时,设∠AOC=2x,则∠COB=3x,则∠AOB=x,得x的值,进而计算出∠AOC与∠AOD的度数,然后得出结论.
分两种情况讨论:
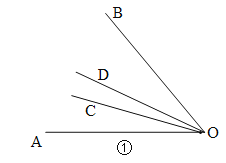
(1)射线OC在∠AOB的内部,如图①;
设∠AOC=2x,则∠COB=3x,则2x+3x=50°,∴x=10°,∠AOC=2x=20°,∠AOD![]() 50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
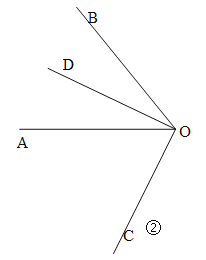
(2)射线OC在∠AOB的外部,如图②.
设∠AOC=2x,则∠COB=3x,则∠AOB=3x﹣2x=x=50°,∴∠AOC=2x=100°
∠AOD=25°,∴∠COD=∠AOC+∠AOD=100°+25°=125°.
综上所述:∠COD=5°或∠COD=125°.

【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.