��Ŀ����
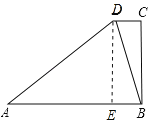
����Ŀ����֪������ABCD�У�AB��CD��BC��AB��AB��AD������BD����ͼa������P�����εıߣ��ӵ�A��B��C��D��A�ƶ������P�ƶ��ľ���Ϊx��BP��y��
��1����֤����A��2��CBD��
��2������P�ӵ�A�ƶ�����Cʱ��y��x�ĺ�����ϵ��ͼ��b���е�����MNQ��ʾ������CD�ij���
��3���ڣ�2��������£���P��A��B��C��D��A�ƶ��Ĺ����У���BDP�Ƿ����Ϊ���������Σ����ܣ������������ʹ��BDPΪ���������ε�x��ȡֵ�������ܣ���˵�����ɣ�

���𰸡���1������������2��1����3����BDP����Ϊ���������Σ���ʹ��BDPΪ���������ε�x��ȡֵΪ��0��3��5��![]() ��
��![]() ��10��9+
��10��9+![]() ��
��
��������
(1)���ݵ�����������������ȿ��Խ�һ��֤����A��2��CBD,
(2) ������������������ȷ��AB=5��AB+BC��8,��ͨ����DE��AB��������ֱ�������ο������CD����.
(3) ������Ŀ����������������ĸ���Ϊ���������ζ��㣬�����з��̽������P��λ�����.
��1��֤������AB��CD��BC��AB��AB��AD��
���ABD����CDB����A+��ADC��180������ABD+��CBD��90������ABD����ADB��
���A+2��ABD��180����2��ABD+2��CBD��180����
���A��2��CBD��
��2���⣺��ͼ��b���ã�AB��5��AB+BC��8��
��BC��3����DE��AB��E����ͼ��ʾ��
��DE��BC��3��CD��BE��
��AD��AB��5��
��AE��![]() ��4��
��4��
��CD��BE��AB��AE��1��
��3���⣺���ܣ��������£�
��������ۣ�
�ٵ�P��AB����ʱ��
��PD��PBʱ��P��A�غϣ�x��0��
��DP��DBʱ��BP��2BE��2��
��AP��3��
��x��3��
��BP��BD��![]() ��
��![]() ʱ��AP��5��
ʱ��AP��5��![]() ��
��
��x��5��![]() ��
��
�ڵ�P��BC��ʱ������PD��PB��
��ʱ��x��5+![]() ��
��![]() ��
��
�۵�P��AD��ʱ��
��BP��BD��![]() ʱ��x��5+3+1+2��10��
ʱ��x��5+3+1+2��10��
��DP��DB��![]() ʱ��x��5+3+1+
ʱ��x��5+3+1+![]() ��9+
��9+![]() ��
��
������������BDP����Ϊ���������Σ���ʹ��BDPΪ���������ε�x��ȡֵΪ��0��3��5��![]() ��
��![]() ��10��9+
��10��9+![]() ��
��

����Ŀ����ͬѧ��������мף���������Ʒ�Ӱ�װ�����۵�һϵ�����⣻
��1��ij��װ������22�����ˣ�ÿ��ÿСʱ����װ120������Ʒ����200������Ʒ����1������Ʒ��Ҫ����2������Ʒװ�䣬Ϊʹÿ���װ�ļ���Ʒ������Ʒ�պ����ã�Ӧ���Ű�װ����Ʒ������Ʒ�Ĺ��˸���������
��2��ij�������е�һ����6000Ԫ����һ���ס���������Ʒ�����м���Ʒ�ļ���������Ʒ������2����30����������Ʒ�Ľ��ۺ��ۼ�����ͼ��ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 22 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
�����н�������ȫ���۳�һ�����Ի�������Ԫ��
���ó��еڶ��ηֱ��Ե�һ��ͬ���Ľ��۹����ڶ����ס���������Ʒ����������Ʒ�ļ����ǵ�һ������Ʒ������3��������Ʒ�ļ������䣬����Ʒ����ԭ�ۼ����ۣ�����Ʒ��ԭ�۵Ļ����ϴ������ۣ��ڶ�����Ʒȫ���۳����õ�������ȵ�һ����õ��������720Ԫ����ڶ�������Ʒ��ԭ�ۻ����ϴ������ۣ�
����Ŀ���������̨�����ʶ�������Ŀ������ͬѧ�ǵĶ������飬Ϊ������ѧ��������飬����������ijУ���꼶����ѧ���Ŀ����Ķ���������������飬�������������֣�ѧ�������Ķ��ı������ٵ���5����������8���������ݵ����������˲�������ͼ������ͼ��ʾ��
���������� | Ƶ���������� | Ƶ�� |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
�ϼ� | 50 | c |
���Ƕ���Ƶ��=![]() �������ɱ������ǿ���֪���������������г�������Ϊ50�˿����Ķ���Ϊ6����ͬѧΪ18�ˣ�������������Ӧ��Ƶ�ʾ���
�������ɱ������ǿ���֪���������������г�������Ϊ50�˿����Ķ���Ϊ6����ͬѧΪ18�ˣ�������������Ӧ��Ƶ�ʾ���![]() =0.36��
=0.36��
��1��ͳ�Ʊ��е�a��b��c��ֵ��
��2���뽫Ƶ���ֲ���ֱ��ͼ����������
��3�������б�����ѧ�������Ķ���ƽ��������
��4������У���꼶����600��ѧ��������Ϊ�������ϵ��������Թ��������У���꼶ѧ�������Ķ���Ϊ7����8����������Ϊ��������д����ļ�����̣�