��Ŀ����
����Ŀ��
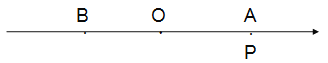
��1��д�������ϵ�B��ʾ���� _______����P��ʾ����________���ú�t�Ĵ���ʽ��ʾ����
��2������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ�ϵ�Q����5�֣�
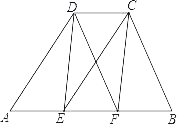
��3����MΪAP���е㣬NΪPB���е㣮��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij�����5�֣�
��4������D��������һ�㣬��D��ʾ������x������̽��ʽ��|x+6|+|x-8|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ���5�֣�
���𰸡���1����B��ʾ������-6����P��ʾ������8-5t����2��7�룻��3��7����4��14��
�������������������1�����ݵ�A�������AB֮��ľ��뼴����õ�B������͵�P�����ꣻ
��2�����ݾ���IJ�Ϊ14�г����̼�����⣻
��3���������ۣ�������P�ڵ�A��B����֮���˶�ʱ��������P�˶�����B�����ʱ�������е�Ķ�����߶εĺͲ������MN��
��4����Ϊ3�����ȥ����ֵ���ţ��������ֲ�ͬ�����ֵ��������۵ó���Сֵ��
�����������1����B��ʾ������-6����P��ʾ������8-5t��
��2�����P�˶�x��ʱ���ڵ�C���ϵ�Q����ͼ��
��AC=5x��BC=3x��
��AC-BC=AB
��5x-3x=14
��ã�x=7��
����P�˶�7��ʱ���ڵ�C���ϵ�Q��
��3��û�б仯�������������
������P�ڵ�A��B����֮���˶�ʱ��
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() ��AP+BP��=
��AP+BP��=![]() AB=7
AB=7
������P�˶�����B�����ʱ��
MN=MP-NP=![]() AP-
AP-![]() BP=
BP=![]() ��AP-BP��=
��AP-BP��=![]() AB=7
AB=7
�����������߶�MN�ij��Ȳ������仯����ֵΪ7
��4��ʽ��|x+6|+|x-8|����Сֵ����СֵΪ14��