题目内容
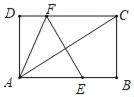
【题目】在平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 在射线
在射线![]() 上,把线段
上,把线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .请根据题意画出图形并完成下列问题:
.请根据题意画出图形并完成下列问题:
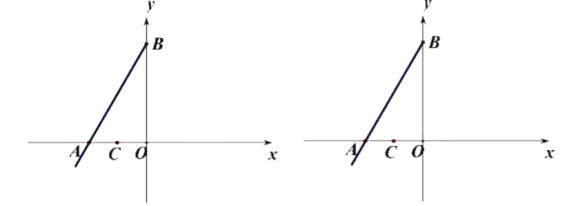
(1)求![]() 的长;
的长;
(2)设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的横坐标
的横坐标![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)﹣5或-1或3.
;(3)﹣5或-1或3.
【解析】
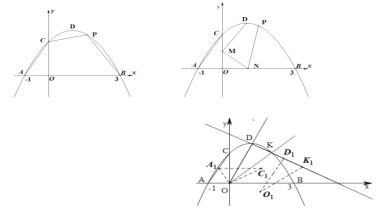
(1)在Rt△ABO中,根据OA=4,∠BAO=60°解直角三角形即可得到AB的长.作图分两种情况:①点D在A的下方,②点D在线段AB上;
(2)分三种情况讨论:①当D在A的下方时,作CM⊥AB于M,EN⊥OA于N.
由点D的横坐标为t,A的横坐标为-4,得出t<-4.用待定系数法求出直线AB的解析式为y![]() x+4
x+4![]() .设D(t,
.设D(t,![]() t+4
t+4![]() ).通过证明△CDM≌△ECN,得到EN=CM,CN=DM.解直角三角形CAM得到AM,CM的长.利用两点间距离公式得到AD
).通过证明△CDM≌△ECN,得到EN=CM,CN=DM.解直角三角形CAM得到AM,CM的长.利用两点间距离公式得到AD![]() .由t<-4,得到AD=﹣8﹣2t,DM=﹣7﹣2t,CN=DM=﹣7﹣2t,ON=﹣5﹣2t,即可得到结论;
.由t<-4,得到AD=﹣8﹣2t,DM=﹣7﹣2t,CN=DM=﹣7﹣2t,ON=﹣5﹣2t,即可得到结论;
②当D在A的上方线段AB上,E在第二象限时,作CM⊥AB于M,EN⊥OA于N.由点D的横坐标为t,A的横坐标为-4,得到t>-4.同①可得:AM=1,CM=![]() ,AD=
,AD=![]() =8+2t,DM=7+2t,CN=DM=7+2t,ON=﹣5﹣2t,即可得到结论;
=8+2t,DM=7+2t,CN=DM=7+2t,ON=﹣5﹣2t,即可得到结论;
③当D在A的上方线段AB上,E在第一象限时,同②可得结论;
(3)连接EF、FC、DF.设EC和DF相交于点H.证明四边形DCFE是菱形,得到H平分DF和EC.设F(x,y).由中点坐标公式可得x,y的值,从而得到F的坐标,表示出![]() ,
,![]() ,
,![]() ,然后分三种情况讨论,解方程即可.
,然后分三种情况讨论,解方程即可.
(1)∵C(﹣2,0),
∴OC=2.
∵C为OA的中点,
∴OA=2OC=4.
∵∠BAO=60°,
∴∠ABO=30°,
∴OB=![]() AC=
AC=![]() ,AB=2AO=8;
,AB=2AO=8;
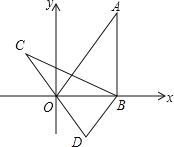
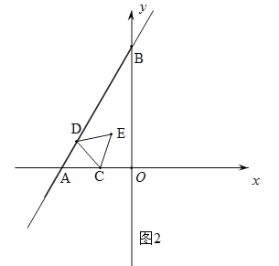
作图分两种情况:①点D在A的下方,如图1;②点D在线段AB上,如图2.
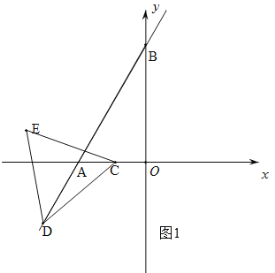
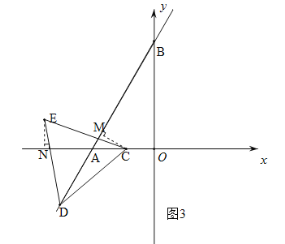
(2)分三种情况讨论:①当D在A的下方时,如图3.
作CM⊥AB于M,EN⊥OA于N.
∵点D的横坐标为t,A的横坐标为-4,
∴t<-4.
∵B(0,4![]() ),A(﹣4,0),
),A(﹣4,0),
∴设直线AB的解析式为![]() ,把A(﹣4,0)代入得:
,把A(﹣4,0)代入得:![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y![]() x+4
x+4![]() .
.
设D(t,![]() t+4
t+4![]() ).
).
∵∠DCE=∠BAC=60°,
∴∠ECN+∠ACD=∠ACD+∠CDM,
∴∠CDM=∠ECN,
在△CDM和△ECN中,
 ,
,
∴△CDM≌△ECN,
∴EN=CM,CN=DM.
∵AC=2,∠CAM=60°,
∴AM=1,CM=![]() .
.
∵D(t,![]() t+4
t+4![]() ),A(-4,0),
),A(-4,0),
∴AD=![]() .
.
∵t<-4,
∴AD=﹣8﹣2t,
∴DM=﹣7﹣2t,
∴CN=DM=﹣7﹣2t,
∴ON=﹣5﹣2t,
∴点E坐标(2t+5,![]() ),
),
∴E点横坐标d=2t+5,
②当D在A的上方线段AB上,E在第二象限时,如图4,作CM⊥AB于M,EN⊥OA于N.
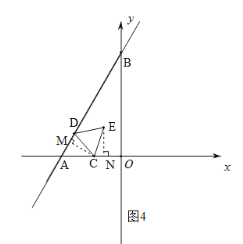
∵点D的横坐标为t,A的横坐标为-4,
∴t>-4.
同①可得:直线AB的解析式为y![]() x+4
x+4![]() ,AM=1,CM=
,AM=1,CM=![]() ,AD=
,AD=![]() .
.
∵t>-4
∴AD=8+2t,DM=7+2t,
∴CN=DM=7+2t,
∴ON=OC-CN=2-(7+2t)=﹣5﹣2t,
∴点E坐标(2t+5,![]() ),
),
∴E点横坐标d=2t+5.
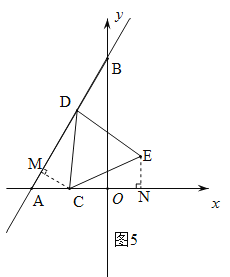
③当D在A的上方线段AB上,E在第一象限时,如图5,作CM⊥AB于M,EN⊥OA于N.
∵点D的横坐标为t,A的横坐标为-4,
∴t>-4.
同②可得:直线AB的解析式为y![]() x+4
x+4![]() ,AM=1,CM=
,AM=1,CM=![]() ,AD=
,AD=![]() .
.
∵t>-4,
∴AD=8+2t,DM=7+2t,
∴CN=DM=7+2t,
∴ON=CN-OC=(7+2t)-2=2t+5,
∴点E坐标(2t+5,![]() ),
),
∴E点横坐标d=2t+5.
综上所述:E点横坐标d=2t+5.
(3)如图6,连接EF、FC、DF.设EC和DF相交于点H.
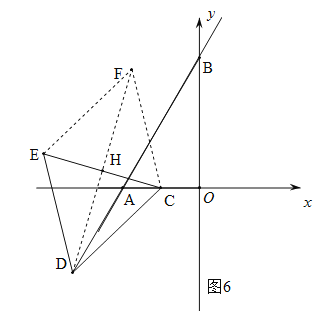
∵D、F关于直线EC对称,
∴DE=EF,DC=CF.
∵△DCE是等边三角形,
∴DE=DC,
∴DE=DC=FC=EF=EC,
∴四边形DCFE是菱形,
∴H平分DF和EC.
设F(x,y).
∵C(﹣2,0),E(2t+5,![]() ),D(t,
),D(t,![]() t+4
t+4![]() ),
),
∴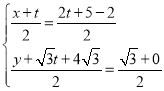 ,
,
解得: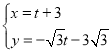 ,
,
∴D关于CE的对称点F点的坐标为(t+3,![]() ).
).
∵A(-4,0),F(t+3,![]() )
)
∴![]() =16,
=16,![]() =
=![]() ,
,
![]() =
=![]() =
=![]() .
.
∵△OAF是等腰三角形,
∴分三种情况讨论:
①当OA=OF时,![]() =
=![]() ,
,
∴![]() ,
,
解得:t=-5或t=-1,
∴d=2t+5=-5或3;
②当OF=AF时,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:t=-5,
∴d=2t+5=-5;
③当AF=OA时,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:t=-3或t=-5,
∴d=2t+5=-1或-5.
综上所述:d的值为-5或-1或3.