题目内容
【题目】如图,抛物线![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 点的右侧),与
点的右侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线的顶点,且
为抛物线的顶点,且![]() .
.
(1)点![]() 为直线
为直线![]() 上方抛物线上一点,求四边形
上方抛物线上一点,求四边形![]() 的面积的最大值;点
的面积的最大值;点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 上的动点,当四边形
上的动点,当四边形![]() 面积取得最大值时,求当线段
面积取得最大值时,求当线段![]() 的值为最小值时点
的值为最小值时点![]() 的坐标.
的坐标.
(2)把![]() 绕点
绕点![]() 旋转一定角度后得到
旋转一定角度后得到![]() ,且点
,且点![]() 恰好在线段
恰好在线段![]() 上,抛物线上的点
上,抛物线上的点![]() 与点
与点![]() 关于抛物线对称轴对称,作
关于抛物线对称轴对称,作![]() ,把
,把![]() 沿直线
沿直线![]() 平移后得到
平移后得到![]() ,在变换过程中是否存在
,在变换过程中是否存在![]() 为等腰三角形,若存在,直接写出此时
为等腰三角形,若存在,直接写出此时![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
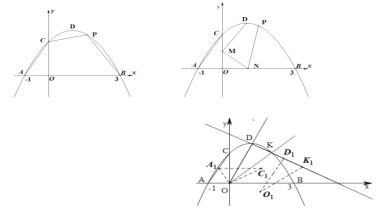
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据题中条件求出直线BC的解析式,设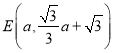 ,
,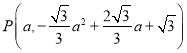 ,四边形ABPC的面积
,四边形ABPC的面积![]() ,得出P点坐标,过
,得出P点坐标,过![]() 点作关于
点作关于![]() 轴的对称点
轴的对称点![]() ,过
,过![]() 点作关于
点作关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,此时
点,此时![]() 的值最小.
的值最小.
(2)先求出D、K、C1的坐标和D1K1线段的长度,利用两点之间的距离公式,表示出![]() 的三边,分三种情况讨论:①当
的三边,分三种情况讨论:①当![]() 时;②当
时;②当![]() ;③
;③![]() 时即可.
时即可.
解:(1) ![]() 抛物线与
抛物线与![]() 轴交于
轴交于![]() 点,
点,
![]()
![]()
∵![]() ,B(3,0)在直线BC上
,B(3,0)在直线BC上
设直线BC的解析式为![]()
代入得: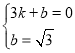
![]()
过![]() 点作
点作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,如图所示
,如图所示
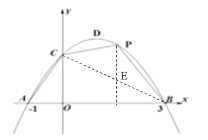
设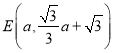 ,
,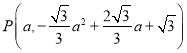
![]()
![]() ,
,
![]() 四边形ABPC的面积:
四边形ABPC的面积:![]()
当![]() 时,
时,![]()
此时![]() .
.
过![]() 点作关于
点作关于![]() 轴的对称点
轴的对称点![]() ,过
,过![]() 点作关于
点作关于![]() 轴的对称点
轴的对称点![]() ,
,
连接![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,此时
点,此时![]() 的值最小.
的值最小.
如图所示:
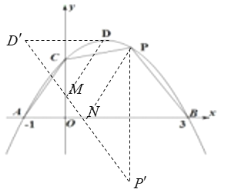
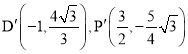
设![]() ,
,
![]()
![]() ,
,
![]()
![]() ;
;
(2)∵![]()
∴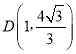
∵点![]() 与点
与点![]() 关于抛物线对称轴对称
关于抛物线对称轴对称
∴![]() ,
,
![]()
∵A(-1,0),![]()
∴![]()
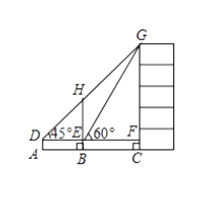
过A1作A1G⊥AO,垂足为G,如图所示
设![]()
∴![]()
解得:![]()
∴OG=![]() ,A1O=2OG
,A1O=2OG
∴∠A1OG=60°
∴∠C1OB=30°
∵CO=OC1=![]()
∴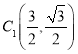
设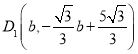 ,则
,则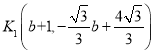
则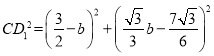
当![]() 时
时

解得:![]()
![]()
当![]() 和
和![]() 时
时
同理可得![]()
∴![]()

【题目】为了解甲、乙两校学生英语口语的学习情况,每个学校随机抽取![]() 个学生进行测试,测试后对学生的成绩进行了整理和分析,绘制成了如下两幅统计图,(数据分组为:
个学生进行测试,测试后对学生的成绩进行了整理和分析,绘制成了如下两幅统计图,(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
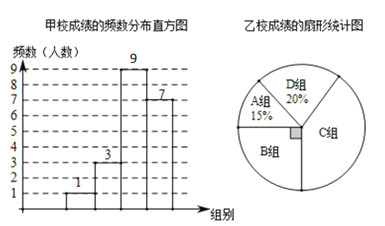
a.甲校学生的测试成绩在![]() 组的是:
组的是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
b.甲、乙两校成绩的平均数,中位数,众数如表:
平均数 | 中位数 | 众数 | |
甲校 | 83.2 | a | 82.5 |
乙校 | 80.6 | 81 | 80 |
根据以上信息,回答下列问题:
(1)扇形统计图中![]() 组所在的圆心角度数为____度,乙校学生的测试成绩位于
组所在的圆心角度数为____度,乙校学生的测试成绩位于![]() 组的人数为___人
组的人数为___人
(2)表格中![]() _________在此次测试中,甲校小明和乙校小华的成绩均为
_________在此次测试中,甲校小明和乙校小华的成绩均为![]() 分,则两位同学在本校测试成绩中的排名更靠前的是________(填小明或小华).
分,则两位同学在本校测试成绩中的排名更靠前的是________(填小明或小华).
(3)假设甲校学生共有![]() 人参加此次测试,估计成绩超过
人参加此次测试,估计成绩超过![]() 分的人数.
分的人数.