题目内容
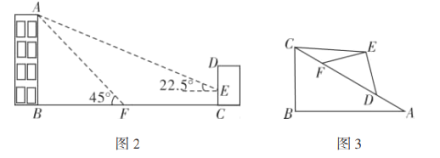
【题目】西安市某中学数学兴趣小组在开展“保护环境，爱护树木”的活动中，利用课外时间测量一棵古树的高，由于树的周围有水池，同学们在低于树基3.3米的一平坝内(如图)．测得树顶A的仰角∠ACB=60°，沿直线BC后退6米到点D，又测得树顶A的仰角∠ADB=45°．若测角仪DE高1.3米，求这棵树的高AM．(结果保留两位小数，
≈1.732)
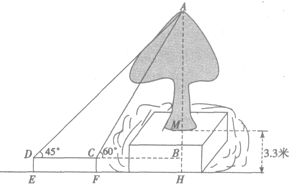
【答案】12.20米
【解析】
可在Rt△ABD和Rt△ABC中，利用已知角的三角函数，用AB表示出BD、BC，根据CD=BD﹣BC=6即可求出AB的长；已知HM、DE的长，易求得BM的值，由AM=AB﹣BM即可求出树的高度．
设AB=x米．
Rt△ABD中，∠ADB=45°，BD=AB=x米．
Rt△ACB中，∠ACB=60°，BC=AB÷tan60°
x米．
CD=BD﹣BC=(1
)x=6，
解得：x=9+3
，
即AB=(9+3)米．
∵BM=HM﹣DE=3.3﹣1.3=2，
∴AM=AB﹣BM=7+3
12.20(米)．
答：这棵树高12.20米．
练习册系列答案
相关题目
