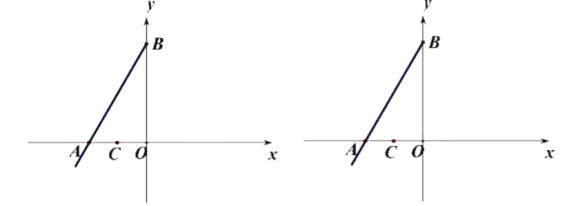题目内容
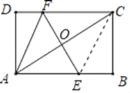
【题目】如图,EF垂直平分矩形ABCD的对角线AC,与AB、CD分别交于点E、F,连接AF.已知AC=4,设AB=x,AF=y,则y关于x的函数关系用图象大致可以表示为( )
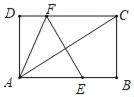
A.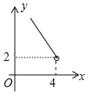 B.
B.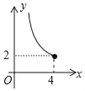 C.
C.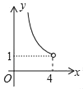 D.
D.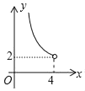
【答案】D
【解析】
先由自变量x的取值,函数y的最小值,排除掉选项B和C,再得出y为关于x的反比例函数,排除A,从而得正确答案.
解:由AB<AC=4可知,B错误;
由EF垂直平分矩形ABCD的对角线AC,得FA=FC,连接EC,则EC=EA,
易证△CFO≌△AEO(ASA)
∴AE=CF=AF=CE=y,BE=AB﹣AE=x﹣y,
∵在直角三角形AEO中,AE>AO=![]() ,
,
∴y>2,排除C;
在直角三角形ABC和直角三角形ECB中,
由勾股定理可得:AC2﹣AB2=EC2﹣BE2,
16﹣x2=y2﹣(x﹣y)2,
化简得:xy=8,
∴![]() ,故y为关于x的反比例函数,排除A;
,故y为关于x的反比例函数,排除A;
综上,D正确.
故选:D.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目