题目内容
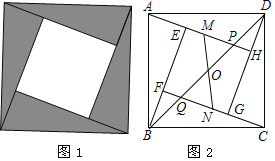
【题目】在![]() 中,∠A=100°,∠B=30°,D为
中,∠A=100°,∠B=30°,D为![]() 边上一点,点
边上一点,点![]() 是射线
是射线![]() 上一点,
上一点,![]() 与射线
与射线![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]()
![]() ,则
,则![]() _______.
_______.
【答案】![]() 或
或![]()
【解析】
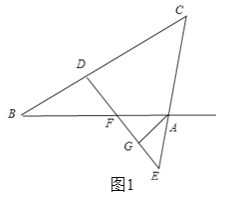
根据三角形的内角和以及外角的性质,得出∠C=50°,∠AFE=∠DFB=50°=∠DEC,从而求得△AEF为等腰三角形,根据等腰三角形的性质求得AG⊥EF,且平分∠EAF,进而求得∠FAG![]() ∠EAF=40°,根据∠CAG=∠CAB+∠FAG或∠CAG=∠FAG即可求得∠CAG的度数.
∠EAF=40°,根据∠CAG=∠CAB+∠FAG或∠CAG=∠FAG即可求得∠CAG的度数.
分两种情况讨论:
①如图,当F点在BA上时.
∵∠A=100°,∠B=30°,
∴∠C=50°,
∴∠EAF=∠B+∠C=80°.
∵∠DEC=∠C=50°,
∴∠CDE=180°﹣50°﹣50°=80°.
∵∠CDE=∠B+∠DFB,
∴∠DFB=80°﹣30°=50°.
∵∠AFE=∠DFB=50°=∠DEC,
∴△AEF为等腰三角形.
∵点G是EF的中点,
∴AG⊥EF,且平分∠EAF,
∴∠FAG![]() ∠EAF=40°,
∠EAF=40°,
∴∠CAG=∠CAB+∠FAG=100°+40°=140°
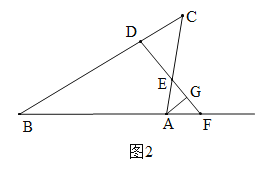
②当点F在BA的延长线上时,如图2,同理可得:∠CAG=∠FAG=40°.
故答案为:140°或40°.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
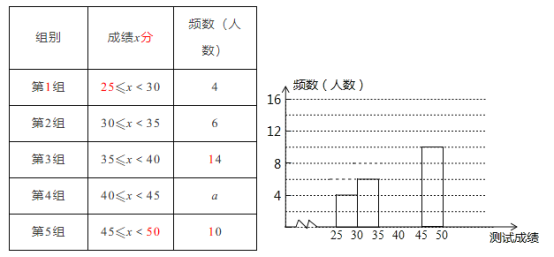
小学教材完全解读系列答案【题目】为了解甲、乙两校学生英语口语的学习情况,每个学校随机抽取![]() 个学生进行测试,测试后对学生的成绩进行了整理和分析,绘制成了如下两幅统计图,(数据分组为:
个学生进行测试,测试后对学生的成绩进行了整理和分析,绘制成了如下两幅统计图,(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
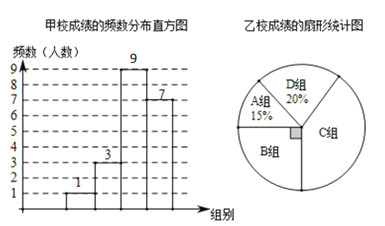
a.甲校学生的测试成绩在![]() 组的是:
组的是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
b.甲、乙两校成绩的平均数,中位数,众数如表:
平均数 | 中位数 | 众数 | |
甲校 | 83.2 | a | 82.5 |
乙校 | 80.6 | 81 | 80 |
根据以上信息,回答下列问题:
(1)扇形统计图中![]() 组所在的圆心角度数为____度,乙校学生的测试成绩位于
组所在的圆心角度数为____度,乙校学生的测试成绩位于![]() 组的人数为___人
组的人数为___人
(2)表格中![]() _________在此次测试中,甲校小明和乙校小华的成绩均为
_________在此次测试中,甲校小明和乙校小华的成绩均为![]() 分,则两位同学在本校测试成绩中的排名更靠前的是________(填小明或小华).
分,则两位同学在本校测试成绩中的排名更靠前的是________(填小明或小华).
(3)假设甲校学生共有![]() 人参加此次测试,估计成绩超过
人参加此次测试,估计成绩超过![]() 分的人数.
分的人数.
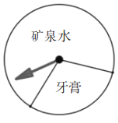
【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物50元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在某一区域就可以获得该区域相对应的奖品.若恰巧落在两区域交界线上,则重新转动转盘.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“矿泉水”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
假如你去转动该转盘一次,你获得牙膏的概率约是______.(用小数表示,结果保留一位小数)