题目内容
【题目】若等腰三角形一腰上的高与另一腰的夹角是45°,则底角的度数为( )
A.67°50'B.67.5°C.22.5°D.22.5°或67.5°
【答案】D
【解析】
分两种情况讨论:(1)当△ABC是锐角三角形时,(2)当△EFG是钝角三角形时,作出相应图形,求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度数.
有两种情况;
(1)如图,当△ABC是锐角三角形时,BD⊥AC于D,
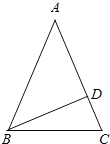
则∠ADB=90°,
已知∠ABD=45°,
∴∠A=90°45°=45°,
∵AB=AC,
∴∠ABC=∠C=![]() ×(180°45°)=67.5°;
×(180°45°)=67.5°;
(2)如图,当△EFG是钝角三角形时,FH⊥EG于H,
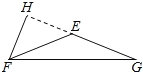
则∠FHE=90°,
已知∠HFE=45°,
∴∠HEF=90°45°=45°,
∴∠FEG=180°45°=135°,
∵EF=EG,
∴∠EFG=∠G=![]() ×(180°135°)=22.5°,
×(180°135°)=22.5°,
综合(1)(2)得:等腰三角形的底角是67.5°或22.5°.
故选:D.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目







