Question

【题目】如图，已知⊙O的半径为2，弦BC的长为，点A为弦BC所对优弧上任意一点（B，C两点除外）.

（1）求∠BAC的度数；

（2）求△ABC面积的最大值.

（参考数据： ，，.）

Answer 1

【答案】解：(1) 解法一

连接OB，OC，过O作OE⊥BC于点E.

∵OE⊥BC，BC=，

∴. ………………1分

在Rt△OBE中，OB=2，∵，

∴, ∴，

∴. ………………4分

解法二

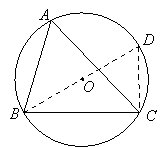
连接BO并延长，交⊙O于点D，连接CD.

∵BD是直径，∴BD=4，.

在Rt△DBC中，,

∴，∴.………………4分

(2) 解法一

因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A落在优弧BC的中点处. ………………5分

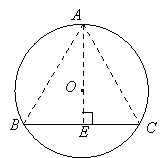
过O作OE⊥BC于E，延长EO交⊙O于点A，则A为优弧BC的中点.连接AB，AC，则AB=AC，.

在Rt△ABE中，∵，

∴，

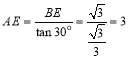∴S△ABC=.

答：△ABC面积的最大值是. ………………7分

解法二

因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积大，此时点A落在优弧BC的中点处. ………………5分

过O作OE⊥BC于E，延长EO交⊙O于点A，则A为优弧BC的中点.连接AB，AC，则AB=AC.

∵, ∴△ABC是等边三角形.

在Rt△ABE中，∵，

∴，

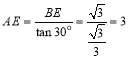∴S△ABC=.

答：△ABC面积的最大值是. ………………7分

【解析】略