题目内容
【题目】如图,△ABC中,AB=AC,点D为BC上一点,以AD为腰作等腰△ADE,且AD=AE, ∠BAC=∠DAE=30°,连接CE,若BD=2,S△DCE=![]() ,则CD的长为 ______.
,则CD的长为 ______.

【答案】![]()
【解析】
过D作DF⊥EC交EC的延长线于F,易证△ABD≌△ACE,得到∠ACE=∠B,根据∠BAC=30°,于是得到∠B+∠ACB=150°,等量代换得到∠BCE=∠ACB+∠ACE=150°,由邻补角的性质得到∠DCF=30°,根据直角三角形的性质得到DF=![]() CD,根据△DCE的面积为
CD,根据△DCE的面积为![]() ,列方程即可得到结论.
,列方程即可得到结论.
过D作DF⊥EC交EC的延长线于F,如图,
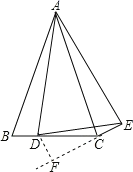
∵∠BAC=∠DAE,
∴∠BAC∠DAC=∠DAE∠DAC,
∴∠BAD=∠EAC,
在△ABD和△ACE中,
AB=AC,∠BAD=∠EAC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B,BD=CE
∵∠BAC=30°,
∴∠B+∠ACB=150°,
∴∠BCE=∠ACB+∠ACE=150°,
∴∠DCF=30°,
∴DF=![]() CD,
CD,
∵CE=BD,△DCE的面积为1,
∴![]() CEDF=
CEDF=![]() BD
BD![]() CD =
CD =![]() =
=![]() ,
,
∴CD=![]()
故答案为:![]() .
.

练习册系列答案
相关题目


