Question

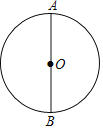
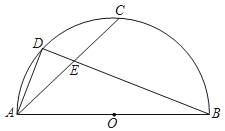
【题目】如图，AB是半圆的直径，点C是的中点，点D是的中点，连接DB、AC交于点E，则∠DAB=_______，_______．

Answer 1

【答案】67.5° ．

【解析】

连接BC、CD，作AF∥CD，交BE于F，根据平行线的性质证得，△ADF是等腰直角三角形，求得，再证，得，．所以．

连接BC、CD，作AF∥CD，交BE于F，

∵，

∴AC=BC．

∵AB是直径，

∴∠ACB=90°，

∴∠CAB=∠CBA=45°．

∵点D是弧AC的中点，

∴可设AD=CD=1，∠ABD=∠DBC=22.5°，

∴∠DAC=∠DBC=22.5°，

∴∠DAB=∠DAC+∠CAB=67.5°

根据平行线的性质得∠AFD=∠CDF=45°，

∴△ADF是等腰直角三角形，

则AF，BF=AF，

∴BD1．

∵∠DAC=∠ABD，∠ADB=∠ADB，

∴△ADE∽△BDA，

∴，即，

∴DE1，，

∴．

故答案为：67.5°，．