题目内容
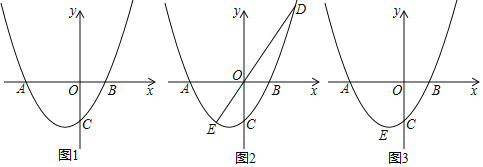
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),动点C从点B出发,沿射线BO方向以每秒1个单位的速度运动,同时动点D从点A出发,沿x轴正方向以每秒1个单位的速度运动,连结CD交直线AB于点E,设点C运动的时间为t秒.

(1)当点C在线段BO上时,
①当OC=5时,求点D的坐标;
②问:在运动过程中,![]() 的值是否为一个不变的值?若是,请求出
的值是否为一个不变的值?若是,请求出![]() 的值,若不是,请说明理由?
的值,若不是,请说明理由?
(2)是否存在t的值,使得△BCE与△DAE全等?若存在,请求出所有满足条件的t的值;不存在,请说明理由.
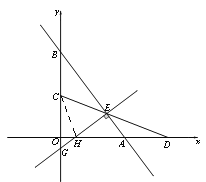
(3)过点E作AB的垂线交x轴于点H,交y轴于点G(如图),当以点C为圆心,CE长 为半径的⊙C经过点G或点H时,请直接写出所有满足条件的t的值.
【答案】(1)①D为(9,0),②存在,![]() 的值不变.
的值不变.![]() ;(2)t=2或50(3)
;(2)t=2或50(3)![]() .
.
【解析】
(1)①OC=5,可求出运动时间t,得到OD的长即可求解;
②过点C作CP∥AB交x轴于点P,利用平行线分线段成比例得到AP=![]() ,再跟进
,再跟进![]() 即可求解;
即可求解;
(2)分①当点C在线段BO上时和②当点C在y轴负半轴上时,根据全等三角形的性质及三角函数的特点列方程求解;
(3)分CE=CG和CE=CH两种情况,分别求出直线E,G,H的坐标,再根据两点之间斜率公式或距离公式列出方程即可求解.
(1)①∵A(6,0),B(0,8)
∴BO=8,AO=6,
当OC=5时,BC=8-5=3=t,
∴OD=OA+AD=6+3=9,
∴D为(9,0).
②![]() 的值不变.
的值不变.
点C运动的时间为t秒
∴BC=t,AD=t,CO=8-t,OD=6+t
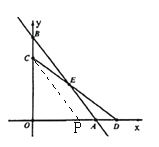
过点C作CP∥AB交x轴于点P,
则![]()
∴![]() ,
,
∴AP=![]() ,
,
∴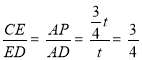 .
.
(2)①当点C在线段BO上时(如图2),
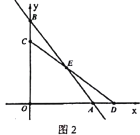
此时∠BCE和∠EAD都是钝角
∵BC=AD=t,∠BEC=∠AED,
∴当∠ABO=∠CDO时,△BCE≌△DAE
∴tan∠ABO=tan∠CDO
∴![]() 即
即![]()
∴t=2;
②当点C在y轴负半轴上时(如图3),
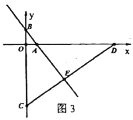
此时,∠BEC,∠AED分别是△DAE,△BCE的外角,
只能∠BEC=∠AED,由∠BEC+∠AED=180°
得∠BEC=∠AED=90°,
∵BC=AD=t,∠CBE=∠ADE
∴△BCE≌△DAE
∴tan∠CBE=tan∠ADE
∴![]() ,即
,即![]()
∴t=50
综上:t=2或50时△BCE与△DAE全等.
(3)①当以点C为圆心,CE长 为半径的⊙C经过点G时,则CE=CG
∵BE⊥EG,
∴CE是△BEG的中线,
∴CG=BC=8-t,OG=t-(8-t)=2t-8
∴G(0,8-2t)
∵A(6,0),B(0,8),求得直线AB的解析式为:y=- ![]() ,kAB=
,kAB= ![]()
∵BE⊥EG
∴kEG= ![]() ,
,
设直线EG的解析式为y=![]() x+b,
x+b,
∵G(0,8-2t)
∴直线EG的解析式为y=![]() x+8-2t
x+8-2t
联立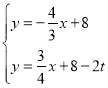 ,解得
,解得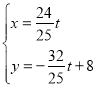
∴E(![]() )
)
∵kCE= kCF
∴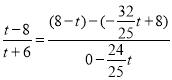
∴![]()
解得t=![]()
②当以点C为圆心,CE长为半径的⊙C经过点H时,则CE=CH
∵C(0,8-t),D(6+t,0)
设CD的解析式为y=kx+b
把C(0,8-t),D(6+t,0)代入得![]() ,解得
,解得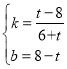
∴CD的解析式为![]()
联立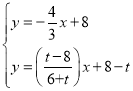 ,解得
,解得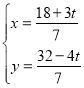
∴E(![]() )
)
∵BE⊥EH
∴kEH= ![]() ,
,
设直线EH的解析式为y=![]() x+b,
x+b,
∵E(![]() )
)
∴直线EH的解析式为y=![]() x+
x+ ![]()
令y=0, ![]() x+
x+ ![]() =0,解得x=
=0,解得x=![]()
∴H(![]() ,0)
,0)
∴CH2=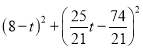 ,CE2=
,CE2=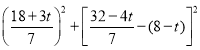 =
=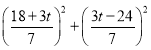
∵CE=CH
∴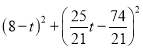 =
=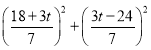
解得t1=8,t2=![]()
综上,t=8或![]() 或
或![]() 以点C为圆心,CE长为半径的⊙C经过点G或点H.
以点C为圆心,CE长为半径的⊙C经过点G或点H.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
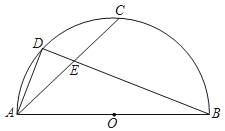
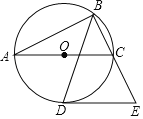
小学生10分钟应用题系列答案【题目】如图,以△ABC的边AC为直径的O恰为△ABC的外接圆,∠ABC的平分线交O于点D,过点D作DE∥AC交BC的延长线于点E
(1)求证:DE是⊙O的切线;
(2)若AB=4![]() ,BC=2
,BC=2![]() ,求DE的长.
,求DE的长.
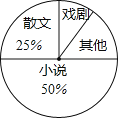
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
(1)计算m= ;
(2)在扇形统计图中,“其他”类所占的百分比为 ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.