Question

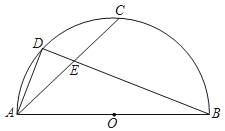
【题目】如图，四边形ABCD是菱形，对角线AC，BD相交于点O，过点D作DH丄AB于H，交AO于G，连接OH．

（1）求证：AGGO＝HGGD；

（2）若AC＝8，BD＝6，求DG的长．

Answer 1

【答案】（1）见解析；（2）DG＝

【解析】

（1）根据菱形的性质得到AC⊥BD，由于DH⊥AB于H，于是得到∠DHA=∠DOG=90°，推出△AGH∽△DGO，根据相似三角形的性质得到，于是得到结论；

（2）根据菱形的性质得到AO=CO=4，BO=DO=3，根据勾股定理得到AB=AD==5，根据相似三角形的性质即可得到结论．

解：（1）证明：∵四边形ABCD是菱形，

∴AC⊥BD，AD＝CD，

∴∠DAC＝∠DCA，

∵DH⊥AB，

∴∠AOD＝∠AHD＝90°，

∵∠AGH＝∠DGO，

∴△AGH∽△DGO，

∴

∴AGGO＝HGGD；

（2）∵四边形ABCD是菱形，AC＝8，DB＝6，

∴OA＝AC＝4，OB＝DB＝3，

∴AB＝＝5，

由（1）△AGH∽△DGO得

∠GAH＝∠GDO

∵∠AOB＝∠DOG＝90°，

∴△AOB∽△DOG，

∴，

∴，

解得：DG＝.