Question

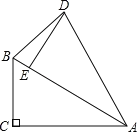
【题目】如图，在Rt△ABC中，∠C=90°，∠ABC=60°，将△ABC绕点A顺时针旋转得△ADE，点C的对应点E恰好落在AB上．

（1）求∠DBC的度数；

（2）当BD时，求AD的长．

Answer 1

【答案】（1）135°；（2）AD1．

【解析】

(1)根据旋转的性质得到三角形ABD为等腰三角形，利用等腰三角形的性质求出∠ABD即可解决问题；

(2)设AD＝AB＝2x，则DE＝AD＝x，AE＝x，利用勾股定理构建方程即可解决问题．

(1)∵∠C=90°，∠ABC=60°，

∴∠BAC=∠DAB=30°．

根据旋转的性质得：AD=AB，

∴∠ABD=∠ADB(180°﹣30°)=75°，

∴∠DBC=∠ABD+∠ABC=75°+60°=135°；

(2)设AD=AB=2x，则DEAD=x，AEx，

∴BE=2xx，

在Rt△BDE中，

∵BD2=DE2+BE2，

∴2=x2+(2xx)2，

解得：x，

∴AD=2x1．