题目内容
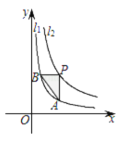
【题目】在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 过点
过点![]() 且与
且与![]() 轴平行,直线
轴平行,直线![]() 过点
过点![]() 且与
且与![]() 轴平行,直线
轴平行,直线![]() 与
与![]() 相交于
相交于![]() .点
.点![]() 为直线
为直线![]() 上一点,反比例函数
上一点,反比例函数![]() 的图象过点
的图象过点![]() 且与直线
且与直线![]() 相交于点
相交于点![]() .
.
(1)若点![]() 与点
与点![]() 重合,求
重合,求![]() 的值;
的值;
(2)连接![]() 、
、![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(3)当![]() 时,在
时,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 是等腰直角三角形?如果存在,直接写出
是等腰直角三角形?如果存在,直接写出![]() 点坐标:若不存在,说明理由.
点坐标:若不存在,说明理由.
【答案】(1)2;(2)点E的坐标为(![]() ,2)或(3,2)时
,2)或(3,2)时![]() 的面积为
的面积为![]() 面积的2倍;(3)当
面积的2倍;(3)当![]() 时,G(0,1)或(0,
时,G(0,1)或(0, ![]() ),此时
),此时![]() 是等腰直角三角形
是等腰直角三角形
【解析】
(1)根据平行线的性质得到点P的坐标,由点E与点P重合得到点E的坐标,将点E的坐标代入![]() 中即可求出k的值;
中即可求出k的值;
(2)根据题意画出图形,用k表示点E及点F的坐标,得到对应线段的长度,分三种情况利用![]() 的面积为
的面积为![]() 面积的2倍分别求出k的值,即可得到点E的坐标;
面积的2倍分别求出k的值,即可得到点E的坐标;
(3)由![]() 知点E在点P的右边,点F在点P的上边,画出图象,设点E的坐标及点F的坐标,分三种情况,根据等腰直角三角形的性质证明全等即可求出答案.
知点E在点P的右边,点F在点P的上边,画出图象,设点E的坐标及点F的坐标,分三种情况,根据等腰直角三角形的性质证明全等即可求出答案.
(1)由题意得点P(1,2),
∵点![]() 与点
与点![]() 重合,
重合,
∴E(1,2),
∵![]() 的图象过点
的图象过点![]() ,
,
∴k=![]() ;
;
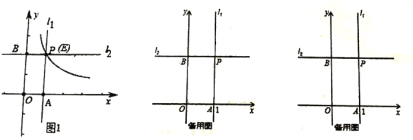
(2)①当0<k<2时,如图1,
根据题意知:四边形OAPB是矩形,BP=1,AP=2,,
∵点E、F都在反比例函数![]() 的图象上,
的图象上,
∴E(![]() ,2),F(1,k),
,2),F(1,k),
∴BE=![]() ,PE=1-
,PE=1-![]() ,AF=k,PF=2-k,
,AF=k,PF=2-k,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
解得![]() ,
, ![]() (舍去),
(舍去),
∴E(![]() ,2);
,2);
当k=2时,△OEF不存在;
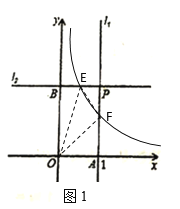
②当k>2时,如图2,过点E作x轴的垂线EC,垂足为C,过点F作y轴的垂线FD,垂足为D,EC和FD相交于点H,则四边形OCHD是矩形,
∵E(![]() ,2),F(1,k),
,2),F(1,k),
∴PE=![]() -1,PF=k-2,
-1,PF=k-2,
∴![]() ,
,
∵四边形PEGF是矩形,
∴![]()
∵![]() ,
,
![]() ,
,
=![]() ,
,
∴![]() =2
=2![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴E(3,2),
综上,点E的坐标为(![]() ,2)或(3,2)时
,2)或(3,2)时![]() 的面积为
的面积为![]() 面积的2倍;
面积的2倍;
(3)存在,
∵k>0,
∴点E在点P的右边,点F在点P的上边,
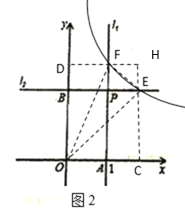
①如图3,∠FEG=90°,EF=EG,
设E(m,2),则F(1,2m),
∵∠EPF=EBG,EF=EG,∠FEP=∠BGE,
∴△FEP≌△EGB,
∴PF=BE,BG=EP,
∴m=2m-2,
∴m=2,
∴BG=PE=1,
∴G(0,1);

②如图4,∠EFG=90°,EF=FG,作FM⊥y轴,
设E(m,2),则F(1,2m),
可得△FEP≌△FMG,
∴FM=FP,MG=EP,
∴2m-2=1,
∴m=![]() ,
,
∴F(1,3),E(![]() ,2),
,2),
∴MG=PE=![]() -1=
-1=![]() ,
,
∴G(0, ![]() );
);

③∠EGF=90°的情况不存在,
综上,当![]() 时,G(0,1)或(0,
时,G(0,1)或(0, ![]() ),此时
),此时![]() 是等腰直角三角形.
是等腰直角三角形.