题目内容
【题目】如图， RtABC 中，BAC 90° ， AB AC ，分别过点 B、C 作过点 A 的直线的垂线BD、CE ，垂足分别为 D、E ，若 BD 4， CE2，则 DE= （_________）
【答案】6
【解析】
首先证明∠DBA=∠CAE，然后再根据AAS定理证明△BDA≌△AEC，根据全等三角形的性质可得DA=CE，AE=DB，进而得到答案．
解：∵∠BAC=90°，
∴∠BAD+∠CAE=90°，
∵BD⊥DE，
∴∠BDA=90°，
∴∠BAD+∠DBA=90°，
∴∠DBA=∠CAE，
∵CE⊥DE，
∴∠E=90°，
在△BDA和△AEC中，
，
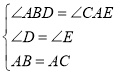∴△BDA≌△AEC（AAS），
∴DA=CE=2，AE=DB=4，
∴ED=6．
故答案为：6
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
