题目内容
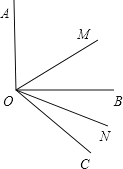
【题目】在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线CM上任意一点,在射线CM上载取CE=BD,连接AD、AE.
(1)如图1,当点D落在线段BC的延长线上时,求证:△ABD≌△ACE;
(2)在(1)的条件下,求出∠ADE的度数;
(3)如图2,当点D落在线段BC(不含端点)上时,作AH⊥BC,垂足为H,作AG⊥EC,垂足为G,连接HG,判断△GHC的形状,并说明现由.

【答案】(1)证明见解析;(2)![]() ;(3)HGC为等边三角形,理由见解析.
;(3)HGC为等边三角形,理由见解析.
【解析】
(1)利用SAS定理证明△ABD≌△ACE;(2)根据全等三角形的性质得到AD=AE,∠CAE=∠BAD,根据等腰三角形的性质、三角形内角和定理计算即可求得∠ADE的度数;
解:(1)∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∵∠ACM=∠ACB,
∴∠ACM=∠ABC,
在△ABD和△ACE中,
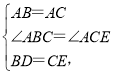
∴△ABD≌△ACE.
(2)由(1)可知,△ABD≌△ACE,
![]()
∴AD=AE,∠BAD=∠CAE.
∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=120°.即∠DAE=120°.
∵AD=AE,
∴∠ADE=∠AED=30°;
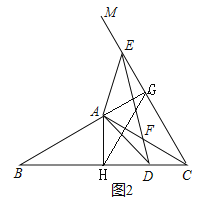
(3)HGC为等边三角形.
理由;![]()
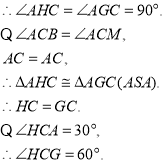
∴HGC为等边三角形.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目