题目内容
已知⊙O的半径为10,弦AB的长为10
,点C在⊙O上,且C点到弦AB所在的直线的距离为5,则以O,A,B,C为顶点的四边形的面积是______.
| 3 |
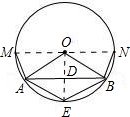
如图,连接OA、OB,过O作垂直于AB的半径OE,交AB于D;
Rt△OAD中,AD=
AB=5
,OA=10;
故∠AOD=60°,OD=5;
①易知DE=OE-OD=5;所以E点符合C点的要求;
此时四边形OAEB的对角线AB、OE互相垂直平分,故四边形OAEB是菱形;
∴S菱形OAEB=
AB•OE=50
;
②过O作平行于AB的直径,交⊙O于M、N,则M、N到AB的距离均为OD=5;
所以M、N也符合C点的要求;
∴S梯形OMAB=S梯形ONBA=
(OM+AB)×OD=25+25
;
故以O,A,B,C为顶点的四边形的面积是50
或25+25
Rt△OAD中,AD=
| 1 |
| 2 |
| 3 |
故∠AOD=60°,OD=5;
①易知DE=OE-OD=5;所以E点符合C点的要求;
此时四边形OAEB的对角线AB、OE互相垂直平分,故四边形OAEB是菱形;
∴S菱形OAEB=
| 1 |
| 2 |
| 3 |
②过O作平行于AB的直径,交⊙O于M、N,则M、N到AB的距离均为OD=5;
所以M、N也符合C点的要求;
∴S梯形OMAB=S梯形ONBA=
| 1 |
| 2 |
| 3 |
故以O,A,B,C为顶点的四边形的面积是50
| 3 |
| 3 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目







