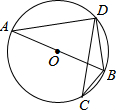
题目内容
如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=4
,ON=1,求⊙O的半径.

(1)求证:AD=AN;
(2)若AB=4
| 2 |

(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
∵
,
∴△ANE≌△ADE,
∴AD=AN;
(2)∵AB=4
,AE⊥CD,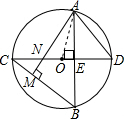
∴AE=2
,
又∵ON=1,
∴设NE=x,则OE=x-1,NE=ED=x,r=OD=OE+ED=2x-1
连结AO,则AO=OD=2x-1,
∵△AOE是直角三角形,AE=2
,OE=x-1,AO=2x-1,
∴(2
)2+(x-1)2=(2x-1)2,解得x=2,
∴r=2x-1=3.
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
∵
|
∴△ANE≌△ADE,
∴AD=AN;
(2)∵AB=4
| 2 |

∴AE=2
| 2 |
又∵ON=1,
∴设NE=x,则OE=x-1,NE=ED=x,r=OD=OE+ED=2x-1
连结AO,则AO=OD=2x-1,
∵△AOE是直角三角形,AE=2
| 2 |
∴(2
| 2 |
∴r=2x-1=3.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目