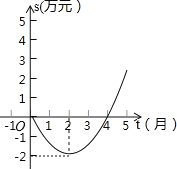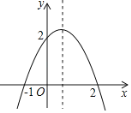��Ŀ����
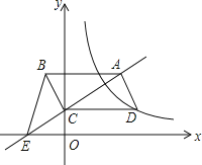
����Ŀ�����Ƕ��壺����������y����y���ϵĵ�M(0��m)Ϊ���ģ����������߹��ڵ�M�ԳƵ�������y���������dz�������y��Ϊ������y���ڵ�M(0��m)��������������������MΪ��������������
(1)��������y=x2-2����ԭ��O(0��0)�����������ߵĽ���ʽ��
(2)��֪������y=ax2+2ax-b(a��0)
����������y������������Ϊy��=bx2-2bx+a2(b��0)�������������������㣬��ǡ�������ǵĶ��㣬��a��b��ֵ���������ĵ����ꣻ
����������y���ڵ�(0��k+12)������������Ϊy1���䶥��ΪA1�����ڵ�(0��k+22)������������Ϊy2���䶥��ΪA2�����������ڵ�(0��k+n2)������������Ϊyn���䶥��ΪAn��(nΪ������)����AnAn+1�ij�(�ú�n��ʽ�ӱ�ʾ)��
���𰸡���1��y'=-x2+2����2����a=3��b=-3���������ĵ�����Ϊ(0��6)����AnAn+1= 4n+2��
��������
��1�����������߶Գ����ʿ�֪������y=ax2+bx+c(a��0)��������������y'��aֵ��Ϊ�෴���������ĶԳƿ�����֪������y=x2-2�Ķ�������(0��-2)������������ߵĶ�������(0��2)���ɵõ����������ߵĽ���ʽ��
��2������������ߵĶ�����������������ߵĶ������꣬�ֱ���������߽���ʽ�У��������a��b��ֵ�����ɵó����ۣ�����������߶������(0��k+n2)��(0��k+(n+1)2)�ĶԳƵ����꣬���ɵó����ۣ�
�⣺��1����������y=x2-2�Ķ���Ϊ(0��-2)��
�������ߵĶ�������(0��-2)����ԭ��(0��0)�ĶԳƵ�Ϊ(0��2)��
�����������ߵĶ�������Ϊ(0��2)��
�����������߿��ڴ�С���䣬����ı䣬�ʶ�����ϵ��Ϊԭ������ϵ����Ϊ�෴����
�����������ߵĽ���ʽΪ��y'=-x2+2��
��2����������y=ax2+2ax-b=a(x+1)2-a-b��
���������ߵĶ�������Ϊ(-1��-a-b)��
��������y������������Ϊy��=bx2-2bx+a2=b(x-1)2+a2-b��
���˺����Ķ�������Ϊ(1��a2-b)��
���������������������㣬��ǡ�������ǵĶ��㣬
�� ��
��
��a=0(��)��a=3��
��b=-3��
��������y�Ķ�������Ϊ(-1��0)��������y�����������ߵĶ�������Ϊ(1��12)��
����������Ϊ���������ߵ��е㣬
���������ĵ�����Ϊ(0��6)��
��������y=ax2+2ax-b�Ķ�������Ϊ(-1��-a-b)��
����(-1��-a-b)���ڵ�(0��k+n2)�ĶԳƵ�Ϊ(1��a+b+2k+2n2)��
��������yn�Ķ�������AnΪ(1��a+b+2k+2n2)��
ͬ����An+1(1��a+b+2k+2(n+1)2)��
��AnAn+1=a+b+2k+2(n+1)2-(a+b+2k+2n2)=4n+2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij��������ȡÿ����������н��Ĵ�ʩ��߹���Ч�ʣ�Ϊ�ƶ�һ��ǡ������������Ӹó���200�������������ȡ20��ͳ����ij�²������£�
ÿ����������� | 260 | 270 | 280 | 290 | 300 | 310 | 350 | 520 |
�� �� | 1 | 1 | 5 | 4 | 3 | 4 | 1 | 1 |
��1����Ӧ����ѧ��ͳ��֪ʶ��Ϊ�ƶ���������Ĺ������ṩ���õIJο����ݣ�
��2������Ϊ�����߽�ÿ��ÿ�˵��������Ϊ��������ʣ�Ϊʲô��
��3�����Ƹó���ȫ�������������ٸ���