题目内容
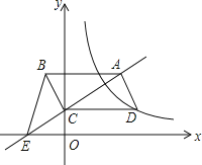
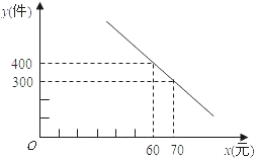
【题目】某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)求y与x之间的函数关系式;
(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
【答案】(1)y=-10x+1000.(2)P=-10x2+1500x-50000;当x=70时,P最大值=6000.
【解析】
(1)设y与x的函数关系式为:y=kx+b,将(60,400)和(70,300)代入即可求出结论;
(2)根据“总利润=总销售额-总成本”即可求出P和x的二次函数关系式,根据题意求出x的取值范围,然后计算出二次函数的对称轴,利用对称轴两侧的增减性即可得出结论.
解:(1)设y与x的函数关系式为:y=kx+b
∵函数图象经过点(60,400)和(70,300)
∴![]() ,
,
解得![]()
∴y=-10x+1000.
(2)P=(x-50)(-10x+1000)=-10x2+1500x-50000
自变量取值范围:50≤x≤70.
∵函数P=-10x2+1500x-50000中,对称轴为x=![]() ,a=-10<0
,a=-10<0
∴函数图象开口向下,对称轴是直线x=75,
∵50≤x≤70,此时P随x的增大而增大,
∴当x=70时,P最大值=6000.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目