ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżčŰÓÚÈęœÇșŻÊęÓĐÈçÏ”Äč«ÊœŁș
ąÙcosŁšŠÁ+ŠÂŁ©ŁœcosŠÁcosŠÂ©sinŠÁsinŠÂŁ»sinŁšŠÁ+ŠÂŁ©ŁœsinŠÁcosŠÂ+cosŠÁsinŠÂŁ»
ąÚtanŁšŠÁ+ŠÂŁ©Łœ![]() Łź
Łź
ąÛÀûÓĂŐâĐ©č«ÊœżÉÒÔœ«Ò»Đ©Č»ÊÇÌŰÊâœÇ”ÄÈęœÇșŻÊęŚȘ»ŻÎȘÌŰÊâœÇ”ÄÈęœÇșŻÊęÀŽÇóÖ”ŁŹÈçtan105ĄăŁœtanŁš45Ąă+60ĄăŁ©Łœ![]() Łœ
Łœ![]() Łœ
Łœ![]() Łœ
Łœ![]() Łœ
Łœ![]() Łź
Łź
žùŸĘÉÏĂæ”ÄÖȘʶŁŹÄăżÉÒÔŃĄÔńÊÊ”±”Äč«ÊœœâŸöÏÂĂæ”ÄÊ”ŒÊÎÊÌâŁș
Łš1Ł©Çócos75Ąă”ÄÖ”Ł»
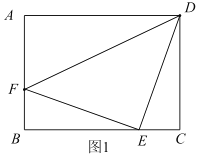
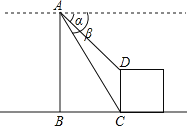
Łš2Ł©ÈçÍŒŁŹÖ±Éę»úÔÚÒ»œšÖțÎïCDÉÏ·œ”Ä”ăAŽŠČâ”ĂœšÖțÎﶄ¶Ë”ăD”Äž©œÇŠÁÎȘ60ĄăŁŹ”Ś¶Ë”ăC”Äž©œÇŠÂÎȘ75ĄăŁŹŽËʱֱÉę»úÓ뜚ÖțÎïCD”ÄËźÆœŸàÀëBCÎȘ42mŁŹÇóœšÖțÎïCD”Ğߣź
ĄŸŽđ°žĄżŁš1Ł©![]() ©
©![]() Ł»Łš2Ł©œšÖțÎïCD”ÄžßÎȘ84ĂŚŁź
Ł»Łš2Ł©œšÖțÎïCD”ÄžßÎȘ84ĂŚŁź
ĄŸœâÎöĄż
Łš1Ł©žùŸĘcosŁšŠÁ+ŠÂŁ©ŁœcosŠÁcosŠÂ©sinŠÁsinŠÂżÉÇócos75Ąă”ÄÖ”Ł»
Łš2Ł©ÏÈÇółöž©œÇŠÂ”ÄŐęÇĐÖ”ŁŹœű¶űžùŸĘBCÇó”ĂABŁŹÔÙÇółöž©œÇŠÁ”ÄŐęÇĐÖ”ŁŹœű¶űžùŸĘBCÇó”ĂAĄąDÁœ”ăŽčÖ±ŸàÀ룏ŚîșóCD”Äł€ŒŽżÉÇó”ĂŁź
œâŁșŁš1Ł©cos75ĄăŁœcosŁš45Ąă+30ĄăŁ©Łœcos45Ąăcos30Ąă©sin45Ąăsin30ĄăŁœ![]() ©
©![]() Ł»
Ł»
Łš2Ł©ĄßŠÂŁœ75ĄăŁŹBCŁœ42ĂŚŁŹ
ĄàABŁœBCtanŠÂŁœ42tan75ĄăŁœ42ĄÁ![]() Łœ42ĄÁ
Łœ42ĄÁ![]() Łœ42Łš
Łœ42Łš![]() +2Ł©ĂŚŁŹ
+2Ł©ĂŚŁŹ
ĄßŠÁŁœ60ĄăŁŹBCŁœ42ĂŚ
ĄàAĄąDŽčÖ±ŸàÀëÎȘBCtanŠÁŁœ42![]() ĂŚŁŹ
ĂŚŁŹ
ĄàCDŁœAB©42![]() Łœ84ĂŚŁź
Łœ84ĂŚŁź
ŽđŁșœšÖțÎïCD”ÄžßÎȘ84ĂŚŁź

 ĂûĐŁÁ·żŒŸíÆÚÄ©łćŽÌŸíÏ”ÁĐŽđ°ž
ĂûĐŁÁ·żŒŸíÆÚÄ©łćŽÌŸíÏ”ÁЎ𰞥ŸÌâÄżĄż±íÖĐËùÁĐ![]() Ąą
Ąą![]() ”Ä7¶ÔÖ”ÊǶțŽÎșŻÊę
”Ä7¶ÔÖ”ÊǶțŽÎșŻÊę![]() ÍŒÏóÉϔĔăËù¶ÔÓŠ”ÄŚű±êŁŹÆäÖĐ
ÍŒÏóÉϔĔăËù¶ÔÓŠ”ÄŚű±êŁŹÆäÖĐ![]()
| Ą |
|
|
|
|
|
|
| Ą |
| Ą | 6 |
| 11 |
| 11 |
| 6 | Ą |
žùŸĘ±íÖĐÌáč©ÔŒĐĆÏąŁŹÓĐÒÔÏÂ4žöĆĐ¶ÏŁșąÙ![]() Ł»ąÚ
Ł»ąÚ![]() Ł»ąÛ”±
Ł»ąÛ”±![]() ʱŁŹ
ʱŁŹ![]() ”ÄÖ”ÊÇ
”ÄÖ”ÊÇ![]() Ł»ąÜ
Ł»ąÜ![]() Ł»ÆäÖĐĆжÏŐęÈ·”ÄÊÇŁš Ł©
Ł»ÆäÖĐĆжÏŐęÈ·”ÄÊÇŁš Ł©
A.ąÙąÚąÛB.ąÙąÚąÜC.ąÙąÛąÜD.ąÚąÛąÜ