题目内容
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 是
是![]() 的中点,
的中点, ![]() 是射线
是射线![]() 上一动点,且
上一动点,且![]() ,连接
,连接![]() ,作
,作![]() ,
, ![]() 交
交![]() 延长线于点
延长线于点![]() .
.
(![]() )如图
)如图![]() ,当点
,当点![]() 在
在![]() 上时,填空:
上时,填空: ![]() __________
__________ ![]() (填“
(填“![]() ”、“
”、“![]() ”或“
”或“![]() ”).
”).
(![]() )如图
)如图![]() ,当点
,当点![]() 在
在![]() 的延长线上时,请根据题意将图形补全,判断
的延长线上时,请根据题意将图形补全,判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.


【答案】(![]() )
)![]() .(
.(![]() )
)![]()
【解析】试题分析:(1)连接EB,由已知条件不难证明△ACD≌△BCE,所以AD=BE,要证明AD=DF,即要证明BE=DF,即要证明△EMB≌△FMD,已知条件MD=MB,∠EMB=∠FMD,只要再证明∠FDM=∠EBC即可,不难证明;(2)连接BE,由已知条件不难证明△ACD≌△BCE,所以EB=AD,要证明AD=DF,即要证明EB=DF,即要证明△EMB≌△FMD,已知条件DM=BM,∠FMD=∠EMB,即要证明∠FDM=∠EBC,不难证明.
试题解析:
(1)连接EB,

∵在△ACD和△BCE中,  ,
,
∴△ACD≌△BCE,
∴∠DAC=∠EBC,EB=AD,
∵∠ADF=90°,
∴∠ADB+∠FDM=90°,
∵∠ACD=90°,
∴∠DAC+∠ADC=90°,
∴∠DAC=∠FDM,
∴∠FDM=∠EBC,
∵M是BD中点,
∴DM=BM,
∵在△EMB和△FMD中,
 ,
,
∴△EMB≌△FMD,
∴EB=DF,
∴AD=DF;
(![]() )AD=DF.
)AD=DF.
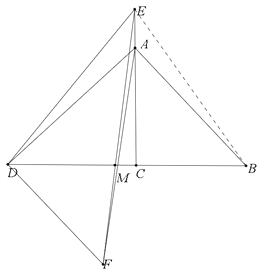
证:连接EB,
∵在△ACD和△ECB中,
 ,
,
∴△ACD≌△BCE,
∴∠DAC=∠EBC,EB=AD,
∵∠ADF=90°,∠ACD=90°,
∴∠ADB+∠FDM=∠DAC+∠ADC=90°,
∴∠DAC=∠FDM,
∴∠FDM=∠EBC,
∵M是BD中点,
∴DM=BM,
∵在△EMB和△FMD中,
 ,
,
∴△EMB≌△FMD,
∴EB=DF,
∴AD=DF.

练习册系列答案
相关题目






