题目内容
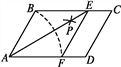
【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若y= ![]() ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少?
【答案】
(1)
解:∵EF⊥DE,
∴∠BEF=90°-∠CED=∠CDE,
又∠B=∠C=90°,
∴△BEF∽△CDE,
∴ ![]()
即
![]()
解得y= ![]() ;
;
(2)
解:由(1)得y= ![]() ,
,
将m=8代入,得y=- ![]()
= ![]()
所以当x=4时,y取得最大值为2;
(3)
解:∵∠DEF=90°,∴只有当DE=EF时,△DEF为等腰三角形,
∴△BEF≌△CDE,
∴BE=CD=m,
此时m=8-x,解方程
![]() =
= ![]() ,
,
得x=6,或x=2,
当x=2时,m=6,
当x=6时,m=2.
【解析】本题把相似三角形与求二次函数解析式联系起来,在解题过程中,充分运用相似三角形对应边的比相等,建立函数关系式.(1)利用互余关系找角相等,证明△BEF∽△CDE,根据对应边的比相等求函数关系式;(2)把m的值代入函数关系式,再求二次函数的最大值;(3)∵∠DEF=90°,只有当DE=EF时,△DEF为等腰三角形,把条件代入即可.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

【题目】某公司在![]() 两仓库分别有机器16台和12台,现要运往甲、乙两地,其中甲地需要15台,乙地需要13台,已知
两仓库分别有机器16台和12台,现要运往甲、乙两地,其中甲地需要15台,乙地需要13台,已知![]() 两地仓库运往甲,乙两地机器的费用如下面的左表所示.
两地仓库运往甲,乙两地机器的费用如下面的左表所示.
![]() 设从A仓库调x台机器去甲地,请用含x的代数式补全下面的右表;
设从A仓库调x台机器去甲地,请用含x的代数式补全下面的右表;
机器调运费用表机器调运方案表
出发地 目的地运费 | A | B | 出发地 目的地机器 | A | B | 合计 | |
甲 | 500 | 300 | 甲地 | x | 15 | ||
乙 | 400 | 600 | 乙地 | 13 | |||
合计 | 16 | 12 | 28 |
![]() 设总运费为y元,求y与x之间的函数解析式,并写出自变量x的取值范围;
设总运费为y元,求y与x之间的函数解析式,并写出自变量x的取值范围;
![]() 由机器调运方案表可知共有n种调运方案,求n的值.
由机器调运方案表可知共有n种调运方案,求n的值.