题目内容
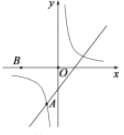
【题目】如图,在ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是菱形,这个条件是( )
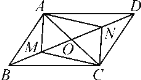
A.OM=![]() ACB.MB=MO
ACB.MB=MO
C.BD⊥ACD.∠AMB=∠CND
【答案】C
【解析】
根据平行四边形的性质可可以得到:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形,由对角线互相垂直的平行四边形可得到菱形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD(平行四边形对角线相互平分),
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵BD⊥AC,
∴MN⊥AC,
∴四边形AMCN是菱形(对角线相互垂直的平行四边形是菱形).
故选C.

练习册系列答案
相关题目