题目内容
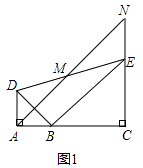
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( ) 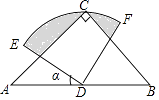
A.由小变大
B.由大变小
C.不变
D.先由小变大,后由大变小
【答案】C
【解析】解:连接CD,
在△ABC中,CA=CB,∠ACB=90°,
∵D为AB的中点,
∴AD=BD=CD,CD平分∠ACB,
过D作DM⊥AC于M,过D作DN⊥BC于N,
∵CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠ACB=∠DNC=90°,
∴四边形CMDN为正方形,
∴∠MDN=90°,
∵∠EDF=90°,
∴∠GDM=∠NDH,
∴∠GDM≌△HDN,
∴S△GDM=S△HDN,
∴S四边形CGDH=S正方形CMDN=CM2=( ![]() AC)2=
AC)2= ![]() AC2,
AC2,
∴四边形CGDH的面积为定值,
∴S阴影=S扇形DEF﹣S四边形CGDH,
∵扇形DEF的圆心角为90°,半径为CD,
∴扇形DEF的面积为定值,
∴当α由小到大变化时,图中阴影部分的面积不变.
故选C.

【考点精析】根据题目的已知条件,利用等腰直角三角形和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).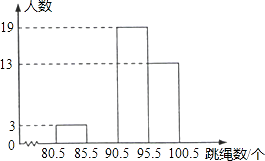
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.