Question

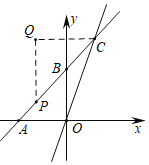
【题目】如图，在平面直角坐标系中，直线11：y＝k1x+3分别与x轴，y轴交于A（﹣3，0），B两点，与直线l2：y＝k2x交于点C，S△AOC＝9．

（1）求tan∠BAO的值；

（2）求出直线l2的解析式；

（3）P为线段AC上一点（不含端点），连接OP，一动点H从点O出发，沿线段OP以每秒1个单位长度的速度运动到P，再沿线段PC以每秒个单位长度的速度运动到点C后停止，请直接写出点H在整个运动过程的最少用时．

Answer 1

【答案】（1）1；（2）y＝2x；（3）6秒．

【解析】

（1）先求直线l1的解析式，从而可以求点B，点A的坐标，求出OA和OB即可求得tan∠BAO＝；

（2）由S△AOC＝9，OA＝3即可求点C的纵坐标，点C是直线l1与直线l2的交点，即可求出直线l2的解析式；

（3）过点C作CJ⊥y轴于J，过点P作PQ⊥CJ于点Q，由题意得，点H在整个运动过程的用时t＝＝OP＋QP，即点H在整个运动过程所用的时间是线段PO与PH的长度之和，也就是点O、P、Q共线时有最小值．

（1）∵直线11：y＝k1x+3经过点A（﹣3，0），

∴0＝﹣3k1+3，即k1＝1且OA＝3

故直线11的解析式为：y＝x+3

∴直线l1：y＝x+3与y轴交点是B（0，3）即OB＝3

故tan∠BAO＝．

（2）∵S△AOC＝9，OA＝3

∴点C到OA也就是到x轴的距离是6，由图可设C（x，6）

∵C（x，6）是直线l1：y＝x+3与直线l2：y＝k2x的交点

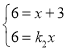∴，解得

故直线l2的解析式是：y＝2x．

（3）如图，过点C作CJ⊥y轴于J，过点P作PQ⊥CJ于点Q，

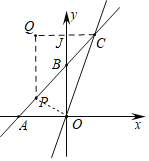
∵动点H从点O出发，沿线段OP以每秒1个单位长度的速度运动到P，遭到沿线段PC以每秒个单位长度的速度运动到点C后停止

∴点H在整个运动过程的用时，

∵tan∠BAO＝知∠BAO＝45°

故∠CPQ＝∠ABO＝45°

∴PQ＝PCcos∠CPQ＝＝

∴即点H在整个运动过程所用的时间是线段PO与PH的长度之和

∴当点P与点B重合，也就是点O、P、Q共线时，OP+QP取得最小值，且（OP+QP）最小＝OJ＝6，

即点H在整个运动过程所用时间的最小值为6秒．