题目内容
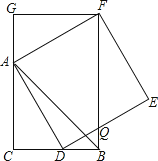
【题目】如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF. 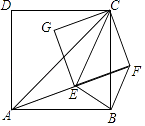
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
【答案】
(1)解:∵四边形ABCD和EFCG均为正方形,
∴ ![]() =
= ![]() ,
,
又∵∠ACE+∠BCE=∠BCF+∠BCE=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF
(2)解:∵△CAE∽△CBF,
∴∠CAE=∠CBF, ![]() ,
,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
又∵ ![]() =
= ![]() ,AE=2
,AE=2
∴ ![]() =
= ![]() ,
,
∴BF= ![]() ,
,
∴EF2=BE2+BF2=3,
∴EF= ![]() ,
,
∵CE2=2EF2=6,
∴CE= ![]() .
.
【解析】(1)首先根据四边形ABCD和EFCG均为正方形,可得 ![]() =
= ![]() ,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

 同步奥数系列答案
同步奥数系列答案