题目内容
【题目】如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P. 
(1)请作出Rt△ABC的外接圆⊙O;(保留作图痕迹,不写作法)
(2)点D在⊙O上吗?说明理由;
(3)试说明:AC平分∠BAD.
【答案】
(1)解:如图,⊙O为所作;
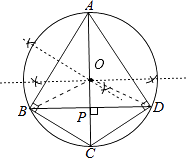
(2)解:点D在⊙O上.理由如下:
连结OD,

∵∠ABC=90°,
∴AC是⊙O的直径,
∵∠ADB=90°,
∴OD= ![]() AC,即OD=OA,
AC,即OD=OA,
∴点D在⊙O上
(3)解:∵AC是⊙O的直径,BD⊥AC,
∴BC=CD,
∴ ![]()
∴∠BAC=∠DAC,
∴AC平分∠BAD
【解析】(1)作AB和BC的垂直平分线,两垂直平分线相交于点O,以OB为半径作⊙O即可;(2)连结OD,先判断AC是⊙O的直径,而∠ADB=90°,根据直角三角形斜边上的中线性质得OD= ![]() AC,即OD=OA,于是根据点与圆的位置关系可判断点D在⊙O上;(3)由于AC是⊙O的直径,BD⊥AC,根据垂径定理得BC=CD,则
AC,即OD=OA,于是根据点与圆的位置关系可判断点D在⊙O上;(3)由于AC是⊙O的直径,BD⊥AC,根据垂径定理得BC=CD,则 ![]() ,然后根据圆周角定理可得∠BAC=∠DAC.
,然后根据圆周角定理可得∠BAC=∠DAC.
【考点精析】认真审题,首先需要了解三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心).

练习册系列答案
相关题目