题目内容
【题目】如图,AC是半圆O的一条弦,以弦AC为折线将弧AC折叠后过圆心O,⊙O的半径为2,则圆中阴影部分的面积为 . 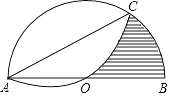
【答案】![]()
【解析】解:过点O作OE⊥AC,交AC于D,连接OC,BC, ∵OD=DE= ![]() OE=
OE= ![]() OA,
OA,
∴∠A=30°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B=60°,
∵OB=OC=2,
∴△OBC是等边三角形,
∴OC=BC,
∴弓形OC面积=弓形BC面积,
∴阴影部分面积=S△OBC= ![]() ×2×
×2× ![]() =
= ![]() .
.
所以答案是: ![]()
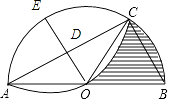
【考点精析】通过灵活运用扇形面积计算公式和翻折变换(折叠问题),掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目