题目内容
【题目】如图，抛物线y=ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC，CD．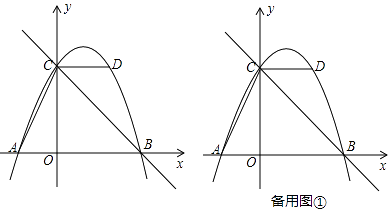
（1）求抛物线的函数表达式；
（2）E是抛物线上的点，求满足∠ECD=∠ACO的点E的坐标；
（3）点M在y轴上且位于点C上方，点N在直线BC上，点P为第一象限内抛物线上一点，若以点C，M，N，P为顶点的四边形是菱形，求菱形的边长．
【答案】
（1）
解：∵抛物线y=ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），
∴设抛物线解析式为y=a（x+2）（x﹣4），
∴﹣8a=4，
∴a=﹣ 
，
∴抛物线解析式为y=﹣ （x+2）（x﹣4）=﹣ x2+x+4
（2）
解：如图1，
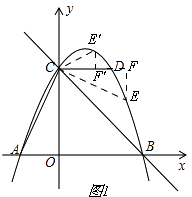
①点E在直线CD上方的抛物线上，记E′，
连接CE′，过E′作E′F′⊥CD，垂足为F′，
由（1）知，OC=4，
∵∠ACO=∠E′CF′，
∴tan∠ACO=tan∠E′CF′，
∴ 
= ，
设线段E′F′=h，则CF′=2h，
∴点E′（2h，h+4）
∵点E′在抛物线上，
∴﹣ （2h）2+2h+4=h+4，
∴h=0（舍）h=
∴E′（1， 
），
②点E在直线CD下方的抛物线上，记E，
连接CE，过E作EF⊥CD，垂足为F，
由（1）知，OC=4，
∵∠ACO=∠ECF，
∴tan∠ACO=tan∠ECF，
∴ 
= ，
设线段EF=h，则CF=2h，
∴点E（2h，4﹣h）
∵点E在抛物线上，
∴﹣ （2h）2+2h+4=4﹣h，
∴h=0（舍）h= 
∴E（3， 
），
点E的坐标为（1， ），（3， ）
（3）
解：①CM为菱形的边，如图2，
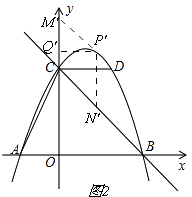
在第一象限内取点P′，过点P′作P′N′∥y轴，交BC于N′，过点P′作P′M′∥BC，交y轴于M′，
∴四边形CM′P′N′是平行四边形，
∵四边形CM′P′N′是菱形，
∴P′M′=P′N′，
过点P′作P′Q′⊥y轴，垂足为Q′，
∵OC=OB，∠BOC=90°，
∴∠OCB=45°，
∴∠P′M′C=45°，
设点P′（m，﹣ m2+m+4），
在Rt△P′M′Q′中，P′Q′=m，P′M′= 
m，
∵B（4，0），C（0，4），
∴直线BC的解析式为y=﹣x+4，
∵P′N′∥y轴，
∴N′（m，﹣m+4），
∴P′N′=﹣ m2+m+4﹣（﹣m+4）=﹣ m2+2m，
∴ m=﹣ m2+2m，
∴m=0（舍）或m=4﹣2 ，
菱形CM′P′N′的边长为 （4﹣2 ）=4 ﹣4．
②CM为菱形的对角线，如图3，
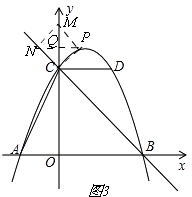
在第一象限内抛物线上取点P，过点P作PM∥BC，
交y轴于点M，连接CP，过点M作MN∥CP，交BC于N，
∴四边形CPMN是平行四边形，连接PN交CM于点Q，
∵四边形CPMN是菱形，
∴PQ⊥CM，∠PCQ=∠NCQ，
∵∠OCB=45°，
∴∠NCQ=45°，
∴∠PCQ=45°，
∴∠CPQ=∠PCQ=45°，
∴PQ=CQ，
设点P（n，﹣ n2+n+4），
∴CQ=n，OQ=n+4，
∴n+4=﹣ n2+n+4，
∴n=0（舍），
∴此种情况不存在．
∴菱形的边长为4 ﹣4
【解析】（1）用待定系数法求出抛物线解析式即可．（2）分①点E在直线CD上方的抛物线上和②点E在直线CD下方的抛物线上两种情况，用三角函数求解即可；（3）分①CM为菱形的边和②CM为菱形的对角线，用菱形的性质进行计算；
【考点精析】根据题目的已知条件，利用二次函数的概念和二次函数的图象的相关知识可以得到问题的答案，需要掌握一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．
