Question

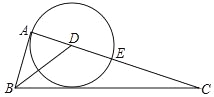
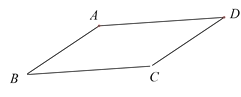
【题目】如图1，△ABC中，∠ACB=90°,∠CAB=30°，△ABD是等边三角形，过点C作CF//BD,交AB于点E，交AD于点F．

（1）求证:△AEF≌△BEC；

（2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，如图2，求sin∠ACH的值．

Answer 1

【答案】(1)详见解析；(2)

【解析】

（1）根据等边三角形及平行线的性质求出AE=CE=BE，再根据ASA即可证明△AEF≌△BEC；

（2）在Rt△ABC中，设BC=1,则AD=AB=2，AC=,设DH=x，则CH=x，在Rt△ACH中，AH2+AC2=HC2，代入求出x的值，再根据三角函数的定义即可求解．

(1)∵△ABD是等边三角形

∴∠D=∠DAB=60°，

∵∠CAB=30°

∴∠FAC=∠DAB+∠CAB=90°=∠ACB

∴AD∥BC

∵CF//BD

∴∠AFC=∠D=60°

∴∠FCA=90°-∠AFC=30°=∠CAB

∴AE=CE，

∵AD∥BC

∴∠ABC=∠DAB=60°

又∠ECB=90°-∠FCA=60°

∴BE=CE

∴AE=BE

又∠FAB=∠EBC=60°，∠AEF=∠BEC,

∴△AEF≌△BEC；

(2) ∵∠BAD=60°，∠CAB=30°

∴∠CAH=90°

在Rt△ABC中，∠CAB=30°，设BC=1,则AB=AD=2，

∴AC==,

设DH=x，则CH=x，AH=2-x

在Rt△ACH中，AH2+AC2=HC2，

即（2-x）2+()2=x2，

解得x=，

∴AH=2-=

∴sin∠ACH==．