题目内容
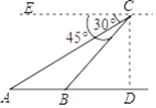
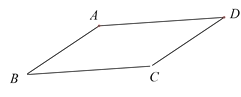
【题目】在ABCD中,∠D=30°,AB<AD.
(1)在AD边上求作一点P,使点P到边AB,BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接BP,若AB=2,求△ABP的面积.
【答案】(1)作图见解析;(2)![]() 的面积为
的面积为![]() .
.
【解析】
(1)以点A为圆心,以AB长为半径画弧,与AD边交于点P即为所作;
(2)如图(见解析),先根据平行四边形的性质、平行线的性质得出![]() ,再根据直角三角形的性质可得BE的长,然后根据三角形的面积公式即可得.
,再根据直角三角形的性质可得BE的长,然后根据三角形的面积公式即可得.
(1)以点A为圆心,以AB长为半径画弧,与AD边交于点P即为所作,如图所示:
理由:连接BP
![]() 四边形ABCD是平行四边形
四边形ABCD是平行四边形
![]()
![]()
由尺规作图可知,![]()
![]()
![]()
![]() 是
是![]() 的角平分线
的角平分线
由角平分线的性质得:点P到边AB,BC的距离相等;
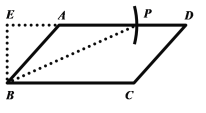
(2)如图,过点B作![]() ,交DA延长线于点E
,交DA延长线于点E
![]() 四边形ABCD是平行四边形
四边形ABCD是平行四边形
![]()
![]()
![]()
![]()
则![]() 的面积为
的面积为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目