Question

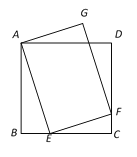
【题目】如图，△ABC内接于⊙O， BC是⊙O 的直径，点A是⊙O上的定点，AD平分∠BAC交⊙O于点D，DG∥BC，交AC延长线于点G.

（1）求证：DG与⊙O相切；

（2）作BE⊥AD于点E，CF⊥AD于点F，试判断线段BE，CF、EF三者之间的数量关系，并证明你的结论(不用尺规作图的方法补全图形).

Answer 1

【答案】（1）见解析；（2）BE＝CF+EF，理由见解析。

【解析】

（1）由AD平分∠BAC得到，再由垂径定理可得DO⊥BC，并进一步得出DG与⊙O相切；

（2）作BE⊥AD于点E，CF⊥AD于点F，连接BD,CD.先证明△BDE≌△DCF，再由全等三角形的性质可得出BE＝CF+EF.因点A是⊙O上的定点，故只需考虑图中情况，不用考虑BE＝CF-EF时的情况.

（1）证明：如图，连接DO并延长到圆上一点N

∵AD平分∠BAC交⊙O于点D，
∴∠BAD=∠DAC，

∴DO⊥BC，
∵DG∥BC，
∴∠GDO=90°，
∴DG与⊙O相切；

（2）BE＝CF+EF，理由如下：

如图，作BE⊥AD于点E，CF⊥AD于点F，连接BD,CD.

∴∠BED=∠DFC=90°

∵BC是直径，，

∴BD=CD, ∠BDC=90°,

∴∠BDE=∠DCF

在△BDE和△DCF中，

∴△BDE≌△DCF（AAS）

∴DE＝CF，BE＝DF

∵DF＝DE+EF

∴BE＝CF+EF