题目内容
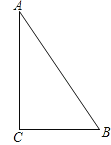
【题目】如图,在一次空中搜寻中,水平飞行的飞机观测到在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为60°的方向上,请你计算当飞机飞临F的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:![]() ≈1.7)
≈1.7)
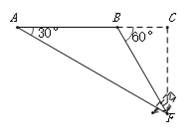
【答案】竖直高度CF约为680米.
【解析】试题分析:根据题意和已知条件易证AB=BF=800米,在Rt△BCF中,根据锐角三角函数求得CF的长即可.
试题解析:
如图所示:
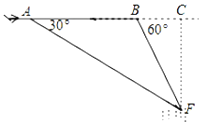
∵∠CBF=60°, ∠CAF=30°,∠CBF=∠CAF+∠BFA,
∴∠BFA=30°,
∴AB=BF,
∵AB=800米,
∴AB=BF=800米,
∵∠BCF=90°,∠CBF=60°,
∴CF=BF·sin60°=800×![]() =400
=400![]() ≈680(m).
≈680(m).
答:竖直高度CF约为680米.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | … |
y | … |
|
|
|
| 3 |
|
|
| m | … |
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .