题目内容
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | … |
y | … |
|
|
|
| 3 |
|
|
| m | … |
求m的值;
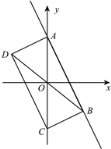
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
【答案】(1)x≠0(2)![]() (3)见解析(4)见解析
(3)见解析(4)见解析
【解析】
(1)根据分母不为零分式有意义,可得答案;
(2)根据自变量与函数值得对应关系,可得答案;
(3)根据描点法画函数图象,可得答案;
(4)根据图象的变化趋势,可得答案;
(1)x≠0 ;
(2)当![]() 时,
时,![]() .
.
∴![]()
(3)该函数的图象如下图所示.
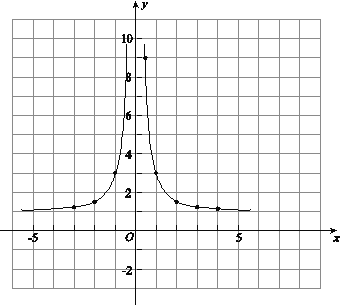
(4)该函数的其它性质:
①当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小 .
②函数的图象与y轴无交点,图象由两部分组成 .(写出一条即可)

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
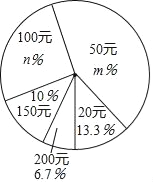
期末好成绩系列答案【题目】某中学在一次爱心捐款活动中,全体同学积极踊跃捐款.现抽查了九年级(1)班全班同学捐款情况,并绘制出如下的统计表和统计图:
捐款(元) | 20 | 50 | 100 | 150 | 200 |
人数(人) | 4 | 12 | 9 | 3 | 2 |
求:(Ⅰ)m=_____,n=_____;
(Ⅱ)求学生捐款数目的众数、中位数和平均数;
(Ⅲ)若该校有学生2500人,估计该校学生共捐款多少元?
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?