题目内容
【题目】先阅读材料：如图（1），在数轴上
示的数为
，
点表示的数为
，则点到点的距离记为
.线段的长可以用右边的数减去左边的数表示，即
.
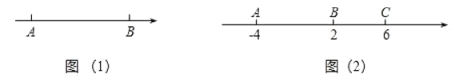
解决问题：如图（2），数轴上点表示的数是-4，点表示的数是2，点
表示的数是6.
（1）若数轴上有一点
，且
，则点表示的数为 ；
（2）点、、开始在数轴上运动，若点以每秒1个单位长度的速度向左运动，同时，若点和点分别以每秒2个单位长度和3个单位长度的速度向右运动，假设
秒钟过后，若点与点之间的距离表示为，点与点之间的距离表示为
，点与点之间的距离表示为
．则点表示的数是 （用含的代数式表示），
（用含的代数式表示）.
（3）请问：
的值是否随着时间的变化而改变？若变化，请说明理由；若不变，请求其值.
【答案】（1）-7或-1；（2）
，
；（3）不变，值为6．
【解析】
（1）设点D表示的数为d，于是得到|﹣4﹣d|=3，求得d=﹣1或﹣7，于是得到结论；
（2）利用题意结合数轴表示出A、B、C三点表示的数，进而可得结论；
（3）根据题意列式计算即可得到结论．
（1）设点D表示的数为d．
∵点A表示的数是﹣4，AD=3，∴|﹣4﹣d|=3，
解得：d=﹣1或﹣7，∴点D表示的数为﹣7或﹣1．
故答案为：﹣7或﹣1；
（2）点A表示的数是﹣4﹣t，点B表示的数是2t+2，点C表示的数是3t+6，∴BC=（3t+6）﹣（2t+2）=t+4．
故答案为：﹣4﹣t，t+4；
（3）不变，值为6．理由如下：
AB=（2t+2）﹣（﹣4﹣t）=2t+2+4+t=3t+6
3BC﹣AB=3（t+4）﹣（3t+6）
=3t+12﹣3t﹣6，
=6．
练习册系列答案
相关题目
