题目内容
【题目】如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sinB=
，AD=1．
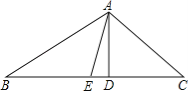
（1）求BC的长；
（2）求tan∠DAE的值．
【答案】（1）
。
（2）
【解析】
（1）先由三角形的高的定义得出∠ADB=∠ADC=90°，再解Rt△ADC，得出DC=1；解Rt△ADB，得出AB=3，根据勾股定理求出BD=
，然后根据BC=BD+DC即可求解。
（2）先由三角形的中线的定义求出CE的值，则DE=CE﹣CD，然后在Rt△ADE中根据正切函数的定义即可求解。
解：（1）在△ABC中，∵AD是BC边上的高，∴∠ADB=∠ADC=90°。
在△ADC中，∵∠ADC=90°，∠C=45°，AD=1，∴DC=AD=1。
在△ADB中，∵∠ADB=90°，sinB=
，AD=1，
∴
。
∴
。
∴
。
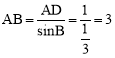（2）∵AE是BC边上的中线，∴CE=
BC=
。
∴DE=CE﹣CD=
。
∴
。
练习册系列答案
相关题目
【题目】注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路，填写表格，并完成本题解答的全过程．如果你选用其他的解题方案，此时，不必填写表格， 只需按照解答题的一般要求，进行解答即可．
某校八年级学生由距博物馆 10km 的学校出发前往参观，一部分同学骑自行车先走，过了20min 后，其余同学乘汽车出发，结果他们同时到达．已知汽车的速度是骑车同学速度 的 2 倍，求骑车同学的速度．
设骑车同学的速度为 xkm / h
（Ⅰ）根据题意，利用速度、时间、路程之间的关系，用含有 x 的式子填写下表：
速度（千米 / 时） | 所用时间（时 ) | 所走的路程（千米） | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
（Ⅱ）列出方程，并求出问题的解．
