题目内容
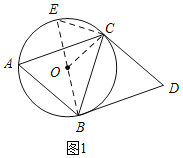
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.

【答案】(1)证明见解析;(2)BD=12,⊙O的半径为![]()
【解析】(1)如图1,作直径BE,半径OC,证明四边形ABDC是平行四边形,得∠A=∠D,由等腰三角形的性质得:∠CBD=∠D=∠A=∠OCE,可得∠EBD=90°,所以BD是⊙O的切线;
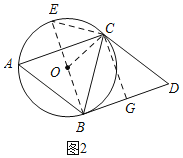
(2)如图2,根据三角函数设EC=3x,EB=5x,则BC=4x根据AB=BC=10=4x,得x的值,求得⊙O的半径为![]() ,作高线CG,根据等腰三角形三线合一得BG=DG,根据三角函数可得结论.
,作高线CG,根据等腰三角形三线合一得BG=DG,根据三角函数可得结论.
(1)如图1,作直径BE,交⊙O于E,连接EC、OC,
则∠BCE=90°,
∴∠OCE+∠OCB=90°,
∵AB∥CD,AB=CD,
∴四边形ABDC是平行四边形,
∴∠A=∠D,
∵OE=OC,
∴∠E=∠OCE,
∵BC=CD,
∴∠CBD=∠D,
∵∠A=∠E,
∴∠CBD=∠D=∠A=∠OCE,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC+∠CBD=90°,
即∠EBD=90°,
∴BD是⊙O的切线;
(2)如图2,∵cos∠BAC=cos∠E=![]() ,
,
设EC=3x,EB=5x,则BC=4x,
∵AB=BC=10=4x,
x=![]() ,
,
∴EB=5x=![]() ,
,
∴⊙O的半径为![]() ,
,
过C作CG⊥BD于G,
∵BC=CD=10,
∴BG=DG,
Rt△CGD中,cos∠D=cos∠BAC=![]() ,
,
∴![]() ,
,
∴DG=6,
∴BD=12.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目