题目内容
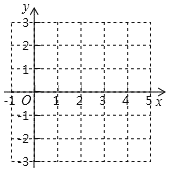
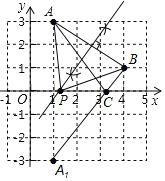
【题目】如图，在直角坐标系中，先描出点A（1，3），点B（4，1）．
（1）描出点A关于x轴的对称点A1的位置，写出A1的坐标 ；
（2）用尺规在x轴上找一点P，使PA＝PB（保留作图痕迹）；
（3）用尺规在x轴上找一点C，使AC+BC的值最小（保留作图痕迹）．
【答案】（1）见解析，A1的坐标（1，﹣3）；（2）见解析；（3）见解析.
【解析】
（1）根据题意，找到A点位置，然后作点A关于x轴对称点A1即可，根据关于x轴对称的两点坐标关系：横坐标相等，纵坐标互为相反数即可求出A1的坐标；
（2）根据题意，作AB的中垂线与x轴的交点即为点P；
（3）连接A1B，交x轴于点C，根据两点之间，线段最短，点C即为所求．
（1）如图所示：A1的坐标（1，﹣3）；
故答案为：（1，﹣3）；
（2）分别以A、B为圆心，以大于
AB为半径作弧，两弧分别交于两点，连接两点的直线与x轴交于点P，如图所示：根据垂直平分线的性质，点P即为所求；
（3）连接A1B，交x轴于点C，如图所示：根据两点之间，线段最短，点C即为所求．
练习册系列答案
相关题目
【题目】某工厂以每千克200元的价格购进甲种原料360千克，用于生产A、B两种产品，生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表：
产品/原料 | A | B |
甲（千克） | 9 | 4 |
乙（千克） | 3 | 10 |
乙种原料的价格为每千克300元，A产品每件售价3000元，B产品每件售价4200元，现将甲种原料全部用完，设生产A产品x件，B产品m件，公司获得的总利润为y元．
（1）写出m与x的关系式；
（2）求y与x的关系式；
（3）若使用乙种原料不超过510千克，生产A种产品多少件时，公司获利最大？最大利润为多少？
