Question

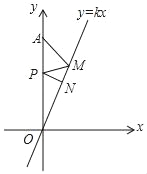
【题目】如图所示，在Rt△ABC中，∠BAC＝90°，∠B＝45°，O为BC中点，如果点M、N分别在线段AB、AC上移动，设AM长为x，CN的长为y，且x、y满足等式＝0（a＞0）．

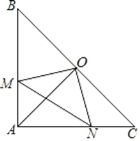
（1）求证：BM＝AN；

（2）请你证明△OMN为等腰直角三角形．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）由等式可得出x=y=a，结合等腰直角三角形的性质，即可证得；
（2）作OE⊥AC，OF⊥AB，通过证明△OFM≌△OEN，可得OM=ON，根据全等三角形的性质，只要证得∠MON=90°，即可证得．

证明：（1）∵x、y满足等式＝0（a＞0），

∴x＝y＝a，即AM＝CN＝a，

∵Rt△ABC中，∠BAC＝90°，∠B＝45°，

∴AB＝AC，

∴BM＝AN；

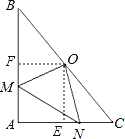
（2）作OE⊥AC，OF⊥AB，

∴∠OFM＝∠ONE＝∠FOE＝90°，

∵点O是BC的中点，

∴OE＝OF＝AB＝AC，AF＝BF，AE＝CE，

∴OF＝OE，AF＝CE，

∴AF﹣AM＝CE﹣CN，

∴MF＝NE，

∴在△OFM和△OEN中 ，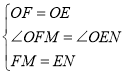

∴△OFM≌△OEN（SAS），

∴OM＝ON，∠MOF＝∠NOE，

∵∠FOM+∠MOE＝90°，

∴∠MOE+∠NOE＝∠MON＝90°，

∴△OMN是等腰直角三角形．