题目内容
【题目】如图，在
中点
是
边上的一点, 
,将
沿
折叠得到
与相交于点
.
(1)求
的度数;
(2)求
的度数.
【答案】（1）
；（2）
【解析】
（1）根据折叠的特点得出∠
∠
，再根据三角形一个外角等于它不相邻两个内角之和，即可得出答案；
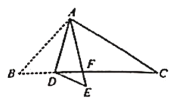
（2）根据已知求出∠ADB的值，再根据折叠的特点得出∠ADE=∠ADB，最后根据∠EDF=∠EDA -∠ADF，即可得出答案．
（1）∵
沿
折叠得到
，
∴∠∠，
∵∠B=50°，∠BAD=30°，
∴∠AFC=∠B+∠BAD+∠DAF
；
（2）∵∠B=50°，∠BAD=30°，
∴∠ADB=180°-50°-30°=100°，
∵沿折叠得到，
∴∠EDA=∠BDA=100°，
∴∠EDF=∠EDA -∠ADF ＝∠EDA –(∠B+∠BAD)
．
练习册系列答案
相关题目
【题目】某工厂以每千克200元的价格购进甲种原料360千克，用于生产A、B两种产品，生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表：
产品/原料 | A | B |
甲（千克） | 9 | 4 |
乙（千克） | 3 | 10 |
乙种原料的价格为每千克300元，A产品每件售价3000元，B产品每件售价4200元，现将甲种原料全部用完，设生产A产品x件，B产品m件，公司获得的总利润为y元．
（1）写出m与x的关系式；
（2）求y与x的关系式；
（3）若使用乙种原料不超过510千克，生产A种产品多少件时，公司获利最大？最大利润为多少？
