题目内容
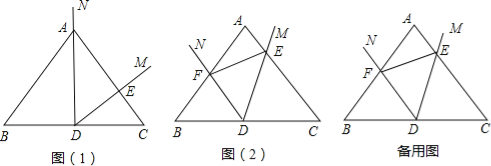
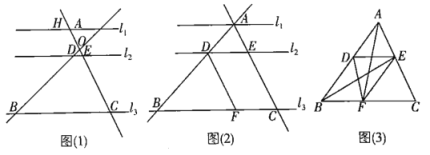
【题目】如图(1)，
，直线AB和CH交于点O，分别交
于D、E两点，已知
，
，
.
(1)尝试探究：在图(1)中，求DB和AD的长；
(2)类比延伸：平移AB使得A与H重合，如图(2)所示，过点D作
，若
，求线段BF的长；
(3)拓展迁移：如图(3)，若
的面积是10，点D、E分别位于AB、CA上，
，点F在BC上且
，
，如果
的面积和四边形FCED的面积相等，求这个相等的面积.
【答案】(1)DB=8；
；(2)
；(3)
.
【解析】
(1)根据
，可得到
,再利用已知条件
，
，
.容易求出AD，BD的长；
（2）当AC移至与HC重合时，利用
可得
,根据(1)中求得的AD、BD的值，即可求出线段BF的长；
（3）要求
的值，就需要求出
．利用
的面积和四边形FCED的面积相等可得
，再推导出四边形BFED是一个平行四边形，然后由
及题中的已知条件得到
，这样就可以得到
与
的面积之比，从而可以解决此题的问题．
【解】(1)∵
，
∴，即
，
∴，
∴
.
(2)∵平移AB使得A与H重合，
∴
，.
∵，
，∴四边形DECF为平行四边形，
∴
.∵，∴
即
，∴.
(3)∵的面积和四边形FCED的面积相等，
，
∴，∴
，又∵
，
∴四边形BDEF为平行四边形，，
∴
，
，
，
即这个相等的面积为6.
【题目】某校九年级甲、乙两班各有学生50人，为了了解这两个班学生身体素质情况，进行了抽样调查，数据整理过程如下，请完成下面数据整理中的问题：
（1）收集数据
从甲、乙两个班中各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：
甲班：65，75，75，80，60，50，75，90，85，65；
乙班：90，55，80，70，55，70，95，80，65，70；
（2）整理描述数据
按如下分数段整理、描述这两组样本数据：
成绩x 人数 班级 | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x＜100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中：m＝ ，n＝ ；
（3）分析数据
①若规定测试成绩在80分（含80分）以上的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生有 人；
②现从甲班指定的3名学生（1男2女），乙班指定的2名学生（1男1女）中分别抽取1名学生去参加身体素质拓展训练，用树状图或列表法求出抽到的2名同学中恰好是1男1女的概率．
