题目内容
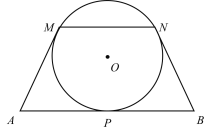
【题目】如图,AB,AM,BN 分别是⊙O 的切线,切点分别为 P,M,N.若 MN∥AB,∠A=60°,AB=6,则⊙O 的半径是( )
A.![]() B.3C.
B.3C.![]()
![]() D.
D.![]()
【答案】D
【解析】
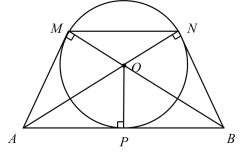
根据题意可判断四边形ABNM为梯形,再由切线的性质可推出∠ABN=60°,从而判定△APO≌△BPO,可得AP=BP=3,在直角△APO中,利用三角函数可解出半径的值.
解:连接OP,OM,OA,OB,ON
∵AB,AM,BN 分别和⊙O 相切,
∴∠AMO=90°,∠APO=90°,
∵MN∥AB,∠A=60°,
∴∠AMN=120°,∠OAB=30°,
∴∠OMN=∠ONM=30°,
∵∠BNO=90°,
∴∠ABN=60°,
∴∠ABO=30°,
在△APO和△BPO中,
 ,
,
△APO≌△BPO(AAS),
∴AP=![]() AB=3,
AB=3,
∴tan∠OAP=tan30°=![]() =
=![]() ,
,
∴OP=![]() ,即半径为
,即半径为![]() .
.
故选D.

练习册系列答案
相关题目
【题目】小尧用“描点法”画二次函数![]() 的 图像,列表如下:
的 图像,列表如下:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | -3 | -4 | -3 | 0 | -5 | … |
(1)由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的 x = ;
(2)在图中画出这个二次函数![]() 的图像;
的图像;
(3)当 y≥5 时,x 的取值范围是 .