题目内容
【题目】(1)(问题发现)
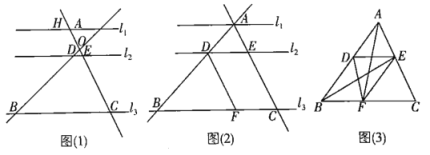
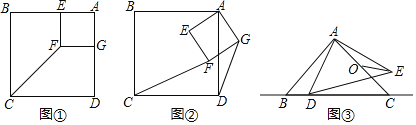
如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD上,连接CF.
填空:①线段CF与DG的数量关系为 ;
②直线CF与DG所夹锐角的度数为 .
(2)(拓展探究)
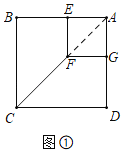
如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.
(3(解决问题)
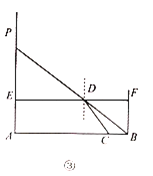
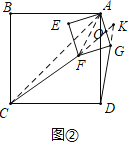
如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC的中点.若点D在直线BC上运动,连接OE,则在点D的运动过程中,线段OE长的最小值为 (直接写出结果).
【答案】(1)①CF=![]() DG;②45°;(2)成立,证明详见解析;(3)
DG;②45°;(2)成立,证明详见解析;(3)![]() .
.
【解析】
(1)【问题发现】连接AF.易证A,F,C三点共线.易知AF=![]() AG.AC=
AG.AC=![]() AD,推出CF=AC﹣AF=
AD,推出CF=AC﹣AF=![]() (AD﹣AG)=
(AD﹣AG)=![]() DG.
DG.
(2)【拓展探究】连接AC,AF,延长CF交DG的延长线于点K,AG交FK于点O.证明△CAF∽△DAG即可解决问题.
(3)【解决问题】证明△BAD≌△CAE,推出∠ACE=∠ABC=45°,可得∠BCE=90°,推出点E的运动轨迹是在射线OCE上,当OE⊥CE时,OE的长最短.
解:(1)【问题发现】如图①中,①线段CF与DG的数量关系为CF=![]() DG;
DG;
②直线CF与DG所夹锐角的度数为45°.
理由:如图①中,连接AF.易证A,F,C三点共线.
∵AF=![]() AG.AC=
AG.AC=![]() AD,
AD,
∴CF=AC﹣AF=![]() (AD﹣AG)=
(AD﹣AG)=![]() DG.
DG.
故答案为CF=![]() DG,45°.
DG,45°.
(2)【拓展探究】结论不变.
理由:连接AC,AF,延长CF交DG的延长线于点K,AG交FK于点O.
∵∠CAD=∠FAG=45°,
∴∠CAF=∠DAG,
∵AC=![]() AD,AF=
AD,AF=![]() AG,
AG,
∴![]() ,
,
∴△CAF∽△DAG,
∴![]() ,∠AFC=∠AGD,
,∠AFC=∠AGD,
∴CF=![]() DG,∠AFO=∠OGK,
DG,∠AFO=∠OGK,
∵∠AOF=∠GOK,
∴∠K=∠FAO=45°.
(3)【解决问题】如图3中,连接EC.
∵AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,∠B=∠ACB=45°,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABC=45°,
∴∠BCE=90°,
∴点E的运动轨迹是在射线CE上,当OE⊥CE时,OE的长最短,易知OE的最小值为![]() ,
,
故答案为![]() .
.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
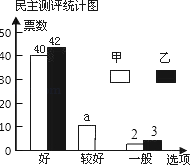
黄冈创优卷系列答案【题目】在校园歌手大赛中,甲、乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:(说明:随机抽取的50名同学每人必须从“好”、“较好”、“一般”中选一票投给每个选手)
A | B | C | D | E | F | |
甲 | 89 | 97 | 90 | 93 | 95 | 94 |
乙 | 89 | 92 | 90 | 97 | 94 | 94 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)学校规定评分标准如下:去掉评委评分中最高和最低分,再算平均分并将平均分与民意测评分按2:3计算最后得分.求甲、乙两位同学的最后得分.(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
【题目】小尧用“描点法”画二次函数![]() 的 图像,列表如下:
的 图像,列表如下:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 5 | 0 | -3 | -4 | -3 | 0 | -5 | … |
(1)由于粗心,小尧算错了其中的一个 y值,请你指出这个算错的y值所对应的 x = ;
(2)在图中画出这个二次函数![]() 的图像;
的图像;
(3)当 y≥5 时,x 的取值范围是 .