ƒøƒ⁄»ð
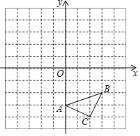
°æƒø°ø∂•µ„Œ™Dµƒ≈◊ŒÔœþy£Ω©Åx2+bx+cΩªx÷·”⁄A°¢B(3£¨0)£¨Ωªy÷·”⁄µ„C£¨÷±œþy£Ω©Å![]() x+mæ≠π˝µ„C£¨Ωªx÷·”⁄E(4£¨0)£Æ
x+mæ≠π˝µ„C£¨Ωªx÷·”⁄E(4£¨0)£Æ
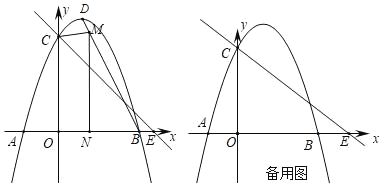
(1)«Û≥ˆ≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
(2)»ÁÕº1£¨µ„MŒ™œþ∂ŒBD…œ≤ª”ÎB°¢D÷ÿ∫œµƒ“ª∏ˆ∂ص„£¨π˝µ„M◊˜x÷·µƒ¥πœþ£¨¥π◊„Œ™N£¨…˵„Mµƒ∫·◊¯±ÍŒ™x£¨Àƒ±þ–ŒOCMNµƒ√ʪ˝Œ™S£¨«ÛS”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£¨≤¢«ÛSµƒ◊Ó¥Û÷µ£ª
(3)µ„PŒ™x÷·µƒ’˝∞Î÷·…œ“ª∏ˆ∂ص„£¨π˝P◊˜x÷·µƒ¥πœþ£¨Ωª÷±œþy£Ω©Å![]() x+m”⁄G£¨Ωª≈◊ŒÔœþ”⁄H£¨¡¨Ω”CH£¨Ω´°˜CGH—ÿCH∑≠’€£¨»Ùµ„Gµƒ∂‘”¶µ„F«°∫√¬‰‘⁄y÷·…œ ±£¨«Î÷±Ω”–¥≥ˆµ„Pµƒ◊¯±Í£Æ
x+m”⁄G£¨Ωª≈◊ŒÔœþ”⁄H£¨¡¨Ω”CH£¨Ω´°˜CGH—ÿCH∑≠’€£¨»Ùµ„Gµƒ∂‘”¶µ„F«°∫√¬‰‘⁄y÷·…œ ±£¨«Î÷±Ω”–¥≥ˆµ„Pµƒ◊¯±Í£Æ
°æ¥∞∏°ø(1)y£Ω©Åx2+2x+3£ª(2)S£Ω©Å(x©Å![]() )2+
)2+![]() £ªµ±x£Ω
£ªµ±x£Ω![]() ±£¨S”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
±£¨S”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £ª(3)¥Ê‘⁄£¨µ„Pµƒ◊¯±ÍŒ™(4£¨0)ªÚ(
£ª(3)¥Ê‘⁄£¨µ„Pµƒ◊¯±ÍŒ™(4£¨0)ªÚ(![]() £¨0).
£¨0).
°æΩ‚Œˆ°ø
£®1£©Ω´µ„E¥˙»Î÷±œþΩ‚Œˆ Ω÷–£¨ø…«Û≥ˆµ„Cµƒ◊¯±Í£¨Ω´µ„C°¢B¥˙»Î≈◊ŒÔœþΩ‚Œˆ Ω÷–£¨ø…«Û≥ˆ≈◊ŒÔœþΩ‚Œˆ Ω£Æ
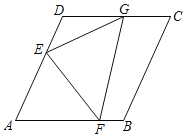
£®2£©Ω´≈◊ŒÔœþΩ‚Œˆ Ω≈‰≥…∂•µ„ Ω£¨ø…«Û≥ˆµ„Dµƒ◊¯±Í£¨…Ë÷±œþBDµƒΩ‚Œˆ Ω£¨¥˙»Îµ„B°¢D£¨ø…«Û≥ˆ÷±œþBDµƒΩ‚Œˆ Ω£¨‘ÚMNø…±Ì 棨‘ÚSø…±Ì æ£Æ
£®3£©…˵„Pµƒ◊¯±Í£¨‘Úµ„Gµƒ◊¯±Íø…±Ì 棨µ„Hµƒ◊¯±Íø…±Ì 棨HG≥§∂»ø…±Ì 棨¿˚”√∑≠’€Õ∆≥ˆCG£ΩHG£¨¡–µ» Ω«ÛΩ‚º¥ø…£Æ
£®1£©Ω´µ„E¥˙»Î÷±œþΩ‚Œˆ Ω÷–£¨
0£Ω©Å![]() °¡4+m£¨
°¡4+m£¨
Ω‚µ√m£Ω3£¨
°ýΩ‚Œˆ ΩŒ™y£Ω©Å![]() x+3£¨
x+3£¨
°ýC(0£¨3)£¨
°þB(3£¨0)£¨
‘Ú”–![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™£∫y£Ω©Åx2+2x+3£ª
£®2£©°þy£Ω©Åx2+2x+3£Ω©Å(x©Å1)2+4£¨
°ýD(1£¨4)£¨
…Ë÷±œþBDµƒΩ‚Œˆ ΩŒ™y£Ωkx+b£¨¥˙»Îµ„B°¢D£¨
![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
°ý÷±œþBDµƒΩ‚Œˆ ΩŒ™y£Ω©Å2x+6£¨
‘Úµ„Mµƒ◊¯±ÍŒ™(x£¨©Å2x+6)£¨
°ýS£Ω(3+6©Å2x)x![]() £Ω©Å(x©Å
£Ω©Å(x©Å![]() )2+
)2+![]() £¨
£¨
°ýµ±x£Ω![]() ±£¨S”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
±£¨S”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £Æ
£Æ
(3)¥Ê‘⁄£¨
»ÁÕºÀ˘ 棨
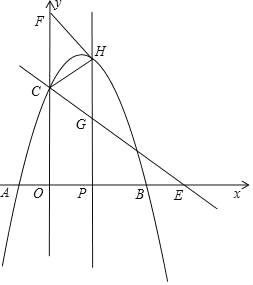
…˵„Pµƒ◊¯±ÍŒ™(t£¨0)£¨
‘Úµ„G(t£¨©Å![]() t+3)£¨H(t£¨©Åt2+2t+3)£¨
t+3)£¨H(t£¨©Åt2+2t+3)£¨
°ýHG£Ω|©Åt2+2t+3©Å(©Å![]() t+3)|£Ω|t2©Å
t+3)|£Ω|t2©Å![]() t|
t|
CG£Ω![]() £Ω
£Ω![]() t£¨
t£¨
°þ°˜CGH—ÿGH∑≠’€£¨Gµƒ∂‘”¶µ„Œ™µ„F£¨F¬‰‘⁄y÷·…œ£¨
∂¯HG°Œy÷·£¨
°ýHG°ŒCF£¨HG£ΩHF£¨CG£ΩCF£¨
°œGHC£Ω°œCHF£¨
°ý°œFCH£Ω°œCHG£¨
°ý°œFCH£Ω°œFHC£¨
°ý°œGCH£Ω°œGHC£¨
°ýCG£ΩHG£¨
°ý|t2©Å![]() t|£Ω
t|£Ω![]() t£¨
t£¨
µ±t2©Å![]() t£Ω
t£Ω![]() t ±£¨
t ±£¨
Ω‚µ√t1£Ω0(…·)£¨t2£Ω4£¨
¥À ±µ„P(4£¨0)£Æ
µ±t2©Å![]() t£Ω©Å
t£Ω©Å![]() t ±£¨
t ±£¨
Ω‚µ√t1£Ω0(…·)£¨t2£Ω![]() £¨
£¨
¥À ±µ„P(![]() £¨0)£Æ
£¨0)£Æ
◊€…œ£¨µ„Pµƒ◊¯±ÍŒ™(4£¨0)ªÚ(![]() £¨0)£Æ
£¨0)£Æ