题目内容
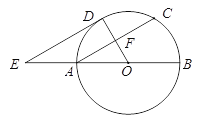
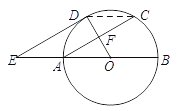
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=2时,求出四边形ACDE的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)根据垂径定理的推论可证明AC⊥OD,根据切线的性质定理证得ED⊥OD,即可证明AC∥DE.(2)连接CD,易证OF=FD,根据SAS可证得△AFO≌△CFD,即可得S四边形ACDE=S△ODE,根据勾股定理求得ED的长,即可得Rt△ODE的面积,从而求得四边形ACDE的面积.
试题解析:
证明:(1)∵F为弦AC(非直径)的中点,∴AF=CF,∴OD⊥AC,
∵DE切⊙O于点D,∴OD⊥DE,∴AC∥DE.
(2)∵AC∥DE,且OA=AE,∴F为OD的中点,即OF=FD,又∵AF=CF,
∠AFO=∠CFD,∴△AFO≌△CFD(SAS),∴S△AFO=S△CFD,∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=2,∴OE=4,∴DE=![]() =2
=2![]()
∴S四边形ACDE=S△ODE=![]() ×OD×OE=
×OD×OE=![]() ×2×2
×2×2![]() =2
=2![]() .
.

【题目】中国杂粮看山西,山西杂粮看忻州,“忻州——中国杂粮之都”近年来打造以“一薯、三麦、四米、五豆”为特色的小杂粮产业,走上了“兴科技、树品牌、强产业广交流、共发展”的新道路.某县为帮助农民进一步提高杂粮播种水平,提升综合生产能力,决定财政拨款45600元购进A,B两种型号的播种机共30台.两种型号播种机的单价和工作效率分别如表:
单价/元 | 工作效率/(公顷/h) | |
A种型号 | 1600 | 4 |
B种型号 | 1480 | 3 |
(1)求购进A,B两种型号的播种机各多少台.
(2)某农场有2000公顷地种植杂粮,计划从县里新购进的播种机中租用两种型号的播种机共15台同时进行播种.若农场的工人每天工作8h,则至少租用A种型号的播种机多少台才能在5天内完成播种工作?