题目内容
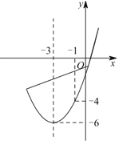
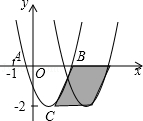
【题目】如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论正确的是 ．（写出所有正确结论的序号）
①b＞0
②a﹣b+c＜0
③阴影部分的面积为4
④若c=﹣1，则b2=4a．
【答案】③④
【解析】
试题①首先根据抛物线开口向上，可得a＞0；然后根据对称轴为x=﹣
＞0，可得b＜0，据此判断即可．②根据抛物线y=ax2+bx+c的图象，可得x=﹣1时，y＞0，即a﹣b+c＞0，据此判断即可．③首先判断出阴影部分是一个平行四边形，然后根据平行四边形的面积=底×高，求出阴影部分的面积是多少即可．④根据函数的最小值是
，判断出c=﹣1时，a、b的关系即可．∵抛物线开口向上，
∴a＞0，又∵对称轴为x=﹣＞0，∴b＜0，∴结论①不正确；
∵x=﹣1时，y＞0，∴a﹣b+c＞0，∴结论②不正确；
∵抛物线向右平移了2个单位，∴平行四边形的底是2，∵函数y=ax2+bx+c的最小值是y=﹣2，
∴平行四边形的高是2，∴阴影部分的面积是：2×2=4，∴结论③正确；
∵，c=﹣1，∴b2=4a，∴结论④正确．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．
（1）求该种水果每次降价的百分率；
（2）从第一次降价的第1天算起，第
天（为整数）的售价、销量及储存和损耗费用的相关信息如表所示．
时间 |
|
|
售价（元/斤） | 第1次降价后的价格 | 第2次降价后的价格 |
销量（斤） |
|
|
储存和损耗费用（元） |
|
|
已知该种水果的进价为4.1元/斤，设销售该水果第（天）的利润为
（元），求与（
）之间的函数解析式，并求出第几天时销售利润最大．
